IntMath forum | Introduction to Geometry
Coordinates of intersection of a tangent from a given point to the circle [Solved!]
Yousuf 26 Sep 2016, 19:31
My question
a) Calculate the length of the tangents from the point `(0, -1)` to the circle `x^2+y^2-10x-4y+12=0`.
b) Calculate the coordinates of the points of intersection of the tangent from (0, -1) to the circle.
c) Deduce that the shape formed by these two tangents and the two radii through the points of contact of the circle and the tangents, is a square.
Relevant page
3. The Circle
What I've done so far
Hi,
Firstly, I want to say thank you to Mr Bourne for the many years of help and support he has given to me in every way, and setting up this brilliant forum which will benefit students from all parts of the world. Lord bless him for the good and grace in him :)
I'm totally stuck on part of a question. Essentially, it entails tangents from a point, and circles. This is the question.
This is what I've done.
Part a) is a breeze. The length of the tangents is `\sqrt(17)`.
Part b) is where I end up in a tangle/dead end.
What I've argued is that to calculate the coordinates of intersection of a line against a circle, we need to be aware that:
`y=mx+c`
`(x-p)^2+(y-q)^2=r^2`
Given that `(0, -1)` is a point:
`-1=m(0)+c \therefore c=-1`
So we have:
`y=mx-1` [1]
`x^2+y^2-10x-4y+12=0` [2]
Substitute [1] into [2]:
`x^2+(mx-1)^2-10x-4(mx-1)+12=0`
`x^2+m^2x^2-2mx+1-10x-4mx+4+12=0`
`x^2(1+m^2)-x(6m+10)+17=0`
`x^2(1+m^2)-2x(3m+5)+17=0`
From this point, I'm pretty much in a hole. I have absolutely no idea how on earth a solution has been found for this equation, but I typed this into WolfAlpha and it came up with at least one gradient for m with the correct x-coordinate.
I know for a fact that I'm on the right trail here, because what I did was I manipulated this problem in GeoGebra and moved the point (0, -1) to a different point namely (10, 5).
`y=mx+c`
`x^2+y^2-10x-4y+12=0`
(10,5) is a point on the line, so:
`5=m(10)+c\therefore c=5-10m`
This then gives:
`y=mx-10m+5`
`x^2+y^2-10x-4y+12=0`
Substituting these together gives a result, but cut short on Wolfram Alpha, it shows that the points of intersection lie at the correct position and for their respective position also advises the gradient of the tangent. These are correct even on GeoGebra.
What I want to very kindly ask is how do I proceed to solving `x^2(1+m^2)-2x(3m+5)+17=0` please?
Thank you so much, really appreciate your time and support :)
- Yousuf.
X
a) Calculate the length of the tangents from the point `(0, -1)` to the circle `x^2+y^2-10x-4y+12=0`.
b) Calculate the coordinates of the points of intersection of the tangent from (0, -1) to the circle.
c) Deduce that the shape formed by these two tangents and the two radii through the points of contact of the circle and the tangents, is a square.
Relevant page
<a href="/plane-analytic-geometry/3-circle.php">3. The Circle</a>
What I've done so far
Hi,
Firstly, I want to say thank you to Mr Bourne for the many years of help and support he has given to me in every way, and setting up this brilliant forum which will benefit students from all parts of the world. Lord bless him for the good and grace in him :)
I'm totally stuck on part of a question. Essentially, it entails tangents from a point, and circles. This is the question.
This is what I've done.
Part a) is a breeze. The length of the tangents is `\sqrt(17)`.
Part b) is where I end up in a tangle/dead end.
What I've argued is that to calculate the coordinates of intersection of a line against a circle, we need to be aware that:
`y=mx+c`
`(x-p)^2+(y-q)^2=r^2`
Given that `(0, -1)` is a point:
`-1=m(0)+c \therefore c=-1`
So we have:
`y=mx-1` [1]
`x^2+y^2-10x-4y+12=0` [2]
Substitute [1] into [2]:
`x^2+(mx-1)^2-10x-4(mx-1)+12=0`
`x^2+m^2x^2-2mx+1-10x-4mx+4+12=0`
`x^2(1+m^2)-x(6m+10)+17=0`
`x^2(1+m^2)-2x(3m+5)+17=0`
From this point, I'm pretty much in a hole. I have absolutely no idea how on earth a solution has been found for this equation, but I typed this into WolfAlpha and it came up with at least one gradient for m with the correct x-coordinate.
I know for a fact that I'm on the right trail here, because what I did was I manipulated this problem in GeoGebra and moved the point (0, -1) to a different point namely (10, 5).
`y=mx+c`
`x^2+y^2-10x-4y+12=0`
(10,5) is a point on the line, so:
`5=m(10)+c\therefore c=5-10m`
This then gives:
`y=mx-10m+5`
`x^2+y^2-10x-4y+12=0`
Substituting these together gives a result, but cut short on Wolfram Alpha, it shows that the points of intersection lie at the correct position and for their respective position also advises the gradient of the tangent. These are correct even on GeoGebra.
What I want to very kindly ask is how do I proceed to solving `x^2(1+m^2)-2x(3m+5)+17=0` please?
Thank you so much, really appreciate your time and support :)
- Yousuf.

Re: Coordinates of intersection of a tangent from a given point to the circle
Murray 27 Sep 2016, 03:59
Hi Yousuf.
You're very welcome ^^.
(1) You didn't indicate how you found the length of the tangent. Much of the question comes out if you do it as follows.
Let the center of the circle be O and the point `(0,-1)` be P, and one of the intersection points with the circle be A, and the other one be B.
Triangle OAP is right angled at A (since a radius and a tangent of a circle are at right angles).
Circle is given by:
`x^2+y^2-10x-4y+12=0`
Find center and radius of circle:
Rearrange:
`x^2-10x + y^2-4y+12=0`
Complete the squares:
`(x^2-10x +25)+ (y^2-4y+4) =25+4-12`
`(x-5)^2+ (y-2)^2 =17`
So our circle has center O`(5,2)` and radius `sqrt(17)`.
Now length PO is
`d=sqrt( (5-0)^2 + (2- {-1})^2 )`
`=sqrt(34)`
So using Pythagoras, the length PA is
`PA= sqrt( (sqrt(34))^2 - (sqrt(17))^2 )`
`=sqrt(34-17)`
`=sqrt(17)`
Using this, we can show the shape is a square (since each side is `sqrt(17)`).
(2) It appears you are only using one of the intersection points, but you can make use of the other to solve your problem.
If the slope of PA `= m`, what is the slope of PB?
X
Hi Yousuf.
You're very welcome ^^.
(1) You didn't indicate how you found the length of the tangent. Much of the question comes out if you do it as follows.
Let the center of the circle be O and the point `(0,-1)` be P, and one of the intersection points with the circle be A, and the other one be B.
Triangle OAP is right angled at A (since a radius and a tangent of a circle are at right angles).
Circle is given by:
`x^2+y^2-10x-4y+12=0`
Find center and radius of circle:
Rearrange:
`x^2-10x + y^2-4y+12=0`
Complete the squares:
`(x^2-10x +25)+ (y^2-4y+4) =25+4-12`
`(x-5)^2+ (y-2)^2 =17`
So our circle has center O`(5,2)` and radius `sqrt(17)`.
Now length PO is
`d=sqrt( (5-0)^2 + (2- {-1})^2 )`
`=sqrt(34)`
So using Pythagoras, the length PA is
`PA= sqrt( (sqrt(34))^2 - (sqrt(17))^2 )`
`=sqrt(34-17)`
`=sqrt(17)`
Using this, we can show the shape is a square (since each side is `sqrt(17)`).
(2) It appears you are only using one of the intersection points, but you can make use of the other to solve your problem.
If the slope of PA `= m`, what is the slope of PB?Re: Coordinates of intersection of a tangent from a given point to the circle
Yousuf 27 Sep 2016, 21:27
Hi sir
Thank you for replying back :)
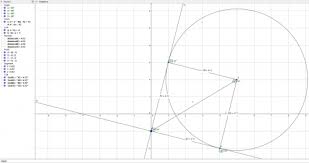
I've attached the working for part a). I figured the part of deducing the square would come later on so I left that bit to focus on the intersection part.
If slope `PA = m`, then slope `PB = - (1/m)` or `PB = -m^-1`
But I still am not quite sure how we solve the resulting equation to get solutions for x and m. I'm not quite sure I've solved an equation quite like this before.

X
Hi sir
Thank you for replying back :)
I've attached the working for part a). I figured the part of deducing the square would come later on so I left that bit to focus on the intersection part.
If slope `PA = m`, then slope `PB = - (1/m)` or `PB = -m^-1`
But I still am not quite sure how we solve the resulting equation to get solutions for x and m. I'm not quite sure I've solved an equation quite like this before.
<img src="/forum/uploads/imf-1956-image3-min.jpg" width="368" height="500" alt="functions-and-graphs" />
Re: Coordinates of intersection of a tangent from a given point to the circle
Murray 30 Sep 2016, 03:35
Hi
I've tried a few ways to get a "nice" approach to solving it, but not yet...
In the meantime, your expression
`x^2(1+m^2)-2x(3m+5)+17=0`
can be written
`(1+m^2)x^2+(-6m-10)x+17=0`
This is a quadratic equation which you can solve for `x` (which is what we need to find, after all).
(It's not pretty, but it will work...)
There's one key bit of insight needed after that to get the needed value(s) for `m`.
Good luck!
X
Hi
I've tried a few ways to get a "nice" approach to solving it, but not yet...
In the meantime, your expression
`x^2(1+m^2)-2x(3m+5)+17=0`
can be written
`(1+m^2)x^2+(-6m-10)x+17=0`
This is a quadratic equation which you can solve for `x` (which is what we need to find, after all).
(It's not pretty, but it will work...)
There's one key bit of insight needed after that to get the needed value(s) for `m`.
Good luck!
Re: Coordinates of intersection of a tangent from a given point to the circle
Yousuf 01 Oct 2016, 13:13
Hi Sir
Just wanted to let you know I solved it!! That little tweak you did with the equation's presentation made all the difference, although the coefficient of x was making a nightmare out of the calculations with there being two minuses. But got there in the end.
Essentially, this is the equation that needs solving:
`(1+m^2)x^2+(-6m-10)x+17=0`
The question is asking us to calculate the points of intersection from the point (0, -1) to the circle. As we can already picture, there will be two distinct points from (0, -1) that will touch the circle. Therefore, there will be two gradients for these two tangents.
To proceed with this, we need to use the discriminant of the quadratic equation because we know that as two there will be two tangents, there will be two gradients.
`D=b^2-4ac`
We also know that as these are tangents, `D=0`
So:
`b^2-4ac=0`
As you said sir, the equation `(1+m^2)x^2+(-6m-10)x+17=0` is a quadratic. Using the coefficients as the respective values of `a`, `b`, and `c`:
`a=1+m^2`
`b=-6m-10`
`c=17`
So:
`(-6m-10)^2-4(1+m^2)(17)=0`
`(-6m-10)(-6m-10)-68(1+m^2)=0`
`36m^2+60m+60m+100-68-68m^2=0`
`36m^2-68m^2+120m+100-68=0`
`-32m^2+120m+32=0`
Initially, to simplify this quadratic, I was repeatedly dividing the equation by 2, and the number of times I did, I saw that dividing by 8 would give:
`-4m^2+15m+4=0`
Or
`-(4m^2-15m-4)=0`
Factorising gives:
`-(4m+1)(m-4)=0`
This means that the gradients are
`m1=-(4m+1)=0`
`m2=-(m-4)=0`
For each gradient:
`m1=-(4m+1)=0`
`-4m-1=0`
`-4m=1`
`4m=-1
`m1\therefore-(1/4)`
Secondly,
`m2=-(m-4)=0`
`-m+4=0`
`-m=-4`
`m=4
`m2\therefore 4`
We now need to find the `x`-coordinates of intersections for both points. We do this by substituting the values of m into `(1+m^2)x^2+(-6m-10)x+17=0`. It is crucial we remember for which ensuing values of `x` belong to the corresponding value of `m`. Because we have already argued using the discriminant that the values of m produce one repeated root, I will be expecting the calculations which follow to produce a conversely repeated root.
Substituting `m=4` into `(1+m^2)x^2+(-6m-10)x+17=0`:
`(1+(4)^2)x^2+(-6(4)-10)x+17=0`
`17x^2-34x+17=0`
`x^2-2x+1=0`
`(x-1)(x-1)=0`
`(x-1)^2=0`
`x\therefore1`
So `x=1` for `m=4'
Next, substituting `m=-(1/4)` into `(1+m^2)x^2+(-6m-10)x+17=0`:
`[1+(-1/4)^2]x^2+[-6(-1/4)-10]x+17=0`
`17/16x^2-17/2x+17=0`
Simplifying this gives:
`17x^2-136x+272=0`
Further simplification of this by dividing by 17:
`x^2-8x+16=0`
Factorising:
`(x-4)(x-4)=0`
`(x-4)^2=0`
`x\therefore4
So `x=4` for `m=-1/4`
Finally, we substitute these resepective values into the equations of each tangents. We know that:
`y=4x-1` for point of intersection `(1,y)`
`y=-1/4x-1` for point of intersection `(4,y)`
For the first one:
`y=4(1)-1`
`y=4-1`
`y\therefore3`
So the first point of intersection is `(1,3)`.
The second one:
`y=-1/4(4)-1`
`y=-1-1`
`y\therefore-2
So the second point of intersection is `(4,-2)`
That solves the problem! Verified through GeoGebra and WolframAlpha!!
Thank you so much again sir for your kind viewing and alteration of the question!!
- Yousuf.
X
Hi Sir
Just wanted to let you know I solved it!! That little tweak you did with the equation's presentation made all the difference, although the coefficient of x was making a nightmare out of the calculations with there being two minuses. But got there in the end.
Essentially, this is the equation that needs solving:
`(1+m^2)x^2+(-6m-10)x+17=0`
The question is asking us to calculate the points of intersection from the point (0, -1) to the circle. As we can already picture, there will be two distinct points from (0, -1) that will touch the circle. Therefore, there will be two gradients for these two tangents.
To proceed with this, we need to use the discriminant of the quadratic equation because we know that as two there will be two tangents, there will be two gradients.
`D=b^2-4ac`
We also know that as these are tangents, `D=0`
So:
`b^2-4ac=0`
As you said sir, the equation `(1+m^2)x^2+(-6m-10)x+17=0` is a quadratic. Using the coefficients as the respective values of `a`, `b`, and `c`:
`a=1+m^2`
`b=-6m-10`
`c=17`
So:
`(-6m-10)^2-4(1+m^2)(17)=0`
`(-6m-10)(-6m-10)-68(1+m^2)=0`
`36m^2+60m+60m+100-68-68m^2=0`
`36m^2-68m^2+120m+100-68=0`
`-32m^2+120m+32=0`
Initially, to simplify this quadratic, I was repeatedly dividing the equation by 2, and the number of times I did, I saw that dividing by 8 would give:
`-4m^2+15m+4=0`
Or
`-(4m^2-15m-4)=0`
Factorising gives:
`-(4m+1)(m-4)=0`
This means that the gradients are
`m1=-(4m+1)=0`
`m2=-(m-4)=0`
For each gradient:
`m1=-(4m+1)=0`
`-4m-1=0`
`-4m=1`
`4m=-1
`m1\therefore-(1/4)`
Secondly,
`m2=-(m-4)=0`
`-m+4=0`
`-m=-4`
`m=4
`m2\therefore 4`
We now need to find the `x`-coordinates of intersections for both points. We do this by substituting the values of m into `(1+m^2)x^2+(-6m-10)x+17=0`. It is crucial we remember for which ensuing values of `x` belong to the corresponding value of `m`. Because we have already argued using the discriminant that the values of m produce one repeated root, I will be expecting the calculations which follow to produce a conversely repeated root.
Substituting `m=4` into `(1+m^2)x^2+(-6m-10)x+17=0`:
`(1+(4)^2)x^2+(-6(4)-10)x+17=0`
`17x^2-34x+17=0`
`x^2-2x+1=0`
`(x-1)(x-1)=0`
`(x-1)^2=0`
`x\therefore1`
So `x=1` for `m=4'
Next, substituting `m=-(1/4)` into `(1+m^2)x^2+(-6m-10)x+17=0`:
`[1+(-1/4)^2]x^2+[-6(-1/4)-10]x+17=0`
`17/16x^2-17/2x+17=0`
Simplifying this gives:
`17x^2-136x+272=0`
Further simplification of this by dividing by 17:
`x^2-8x+16=0`
Factorising:
`(x-4)(x-4)=0`
`(x-4)^2=0`
`x\therefore4
So `x=4` for `m=-1/4`
Finally, we substitute these resepective values into the equations of each tangents. We know that:
`y=4x-1` for point of intersection `(1,y)`
`y=-1/4x-1` for point of intersection `(4,y)`
For the first one:
`y=4(1)-1`
`y=4-1`
`y\therefore3`
So the first point of intersection is `(1,3)`.
The second one:
`y=-1/4(4)-1`
`y=-1-1`
`y\therefore-2
So the second point of intersection is `(4,-2)`
That solves the problem! Verified through GeoGebra and WolframAlpha!!
Thank you so much again sir for your kind viewing and alteration of the question!!
- Yousuf.
Re: Coordinates of intersection of a tangent from a given point to the circle
Murray 01 Oct 2016, 20:26
Good work! You went straight for the "one bit of insight" I was talking about. ^^
Just one small comment. In words, we would say "Therefore y equals negative 2." So in math symbols, we should put
`:.y=-2`,
not
`y:.-2`, since this is missing a verb.
All the best.
X
Good work! You went straight for the "one bit of insight" I was talking about. ^^
Just one small comment. In words, we would say "Therefore y equals negative 2." So in math symbols, we should put
`:.y=-2`,
not
`y:.-2`, since this is missing a verb.
All the best.
Re: Coordinates of intersection of a tangent from a given point to the circle
drapp 11 Dec 2016, 09:58
A great problem for critical thinking. One question, in solving the quadratic it is said that the Discriminant must be zero because the two lines are tangents. Please explain. Thanks
X
A great problem for critical thinking. One question, in solving the quadratic it is said that the Discriminant must be zero because the two lines are tangents. Please explain. Thanks
Re: Coordinates of intersection of a tangent from a given point to the circle
Murray 12 Dec 2016, 10:13
@drapp: It follows from the required symmetry of the solution. If the discriminant was NOT zero, then we would have "messy" parts left over in the expressions for `m1` and `m2` (they would not have the property `m1m2 = -1`.
If it's still not clear, try some values where the discriminant is not 0 - they won't work!
X
@drapp: It follows from the required symmetry of the solution. If the discriminant was NOT zero, then we would have "messy" parts left over in the expressions for `m1` and `m2` (they would not have the property `m1m2 = -1`.
If it's still not clear, try some values where the discriminant is not 0 - they won't work!
Re: Coordinates of intersection of a tangent from a given point to the circle
drapp 13 Dec 2016, 06:35
thanks. I guess another way to say it that lines intersecting the circle that are not tangents would intersect in 4 locations, and D=0 gives the two we are looking for. Could the problem also be solved by finding the equation of the line that goes through AB and solving as an intersection with the circle. Given we proved that a square exists, a point on the line AB would be the midpoint (2.5, 0.5) of CP and its slope -1/m of CP, = -5/3.
Think I'll give it a try. Thanks.
Any other interesting problems like this?
X
thanks. I guess another way to say it that lines intersecting the circle that are not tangents would intersect in 4 locations, and D=0 gives the two we are looking for. Could the problem also be solved by finding the equation of the line that goes through AB and solving as an intersection with the circle. Given we proved that a square exists, a point on the line AB would be the midpoint (2.5, 0.5) of CP and its slope -1/m of CP, = -5/3.
Think I'll give it a try. Thanks.
Any other interesting problems like this?
Re: Coordinates of intersection of a tangent from a given point to the circle
drapp 13 Dec 2016, 07:28
It works. The Algebra is laborious by either method, but that's the fun of it!
X
It works. The Algebra is laborious by either method, but that's the fun of it!
Related Functions and Graphs questions
- Ratio of line segments [Solved!]
Given: the coordinates of the endpoints of line segment AC and the fact that a... phinah 31 Aug 2018, 02:15
- Not getting how to calculate function equation from graph [Solved!]
For MR513, I'm trying to find out value of x(alcohol content) with help of Y(result... HarshalDalal 02 May 2016, 06:41
- Domain and range [Solved!]
you didn't tell how to find domain and ravge of a given function. tell... shaikshavali 11 Dec 2015, 07:43
- How to obtain 0.84? [Solved!]
In Example 1 on the page, how do you obtain 0.84? Please show calculation for... L.Aureli 18 Dec 2015, 11:03
- What is the function for the number 8? [Solved!]
what is the function of the #8 Sherry 04 Oct 2015, 05:05
Functions and Graphs lessons on IntMath
top

