Domain and Range of a Function
Definitions of Domain and Range
Domain
Domain and Range Worksheet
Download this Domain and Range worksheet with 10 questions and answers as a practice test.
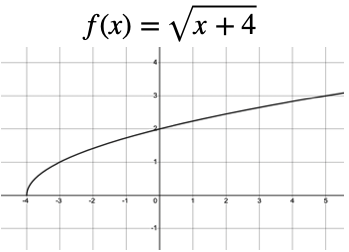
The domain of a function is the complete set of possible values of the independent variable.
In plain English, this definition means:
The domain is the set of all possible x-values which will make the function "work", and will output real y-values.
When finding the domain, remember:
- The denominator (bottom) of a fraction cannot be zero
- The number under a square root sign must be positive in this section
Domain & Range Math Problem Solver
This tool combines the power of mathematical computation engine that excels at solving mathematical formulas with the power of GPT large language models to parse and generate natural language. This creates math problem solver thats more accurate than ChatGPT, more flexible than a calculator, and faster answers than a human tutor.
Domain and Range Interactive
After finishing this lesson head over to our interactive calculator to help you find the Domain and Range of a Fuction.
Example 1a
Here is the graph of `y = sqrt(x+4)`:
The domain of this function is `x ≥ −4`, since x cannot be less than ` −4`. To see why, try out some numbers less than `−4` (like ` −5` or ` −10`) and some more than `−4` (like ` −2` or `8`) in your calculator. The only ones that "work" and give us an answer are the ones greater than or equal to ` −4`. This will make the number under the square root positive.
Notes:
- The enclosed (colored-in) circle on the point `(-4, 0)`. This indicates that the domain "starts" at this point.
- We saw how to draw similar graphs in section 4, Graph of a Function. For a more advanced discussion, see also How to draw y^2 = x − 2.
How to find the domain
In general, we determine the domain of each function by looking for those values of the independent variable (usually x) which we are allowed to use. (Usually we have to avoid 0 on the bottom of a fraction, or negative values under the square root sign).
Range
The range of a function is the complete set of all possible resulting values of the dependent variable (y, usually), after we have substituted the domain.
In plain English, the definition means:
The range is the resulting y-values we get after substituting all the possible x-values.
How to find the range
- The range of a function is the spread of possible y-values (minimum y-value to maximum y-value)
- Substitute different x-values into the expression for y to see what is happening. (Ask yourself: Is y always positive? Always negative? Or maybe not equal to certain values?)
- Make sure you look for minimum and maximum values of y.
- Draw a sketch! In math, it's very true that a picture is worth a thousand words.
Example 1b
Let's return to the example above, `y = sqrt(x + 4)`.
We notice the curve is either on or above the horizontal axis. No matter what value of x we try, we will always get a zero or positive value of y. We say the range in this case is y ≥ 0.
The curve goes on forever vertically, beyond what is shown on the graph, so the range is all non-negative values of `y`.
Example 2
The graph of the curve y = sin x shows the range to be betweeen −1 and 1.
The domain of y = sin x is "all values of x", since there are no restrictions on the values for x. (Put any number into the "sin" function in your calculator. Any number should work, and will give you a final answer between −1 and 1.)
From the calculator experiment, and from observing the curve, we can see the range is y betweeen −1 and 1. We could write this as −1 ≤ y ≤ 1.
Where did this graph come from? We learn about sin and cos graphs later in Graphs of sin x and cos x
Note 1: Because we are assuming that only real numbers are to be used for the x-values, numbers that lead to division by zero or to imaginary numbers (which arise from finding the square root of a negative number) are not included. The Complex Numbers chapter explains more about imaginary numbers, but we do not include such numbers in this chapter.
Note 2: When doing square root examples, many people ask, "Don't we get 2 answers, one positive and one negative when we find a square root?" A square root has at most one value, not two. See this discussion: Square Root 16 - how many answers?
Note 3: We are talking about the domain and range of functions, which have at most one y-value for each x-value, not relations (which can have more than one.).
Finding domain and range without using a graph
It's always a lot easier to work out the domain and range when reading it off the graph (but we must make sure we zoom in and out of the graph to make sure we see everything we need to see). However, we don't always have access to graphing software, and sketching a graph usually requires knowing about discontinuities and so on first anyway.
As meantioned earlier, the key things to check for are:
- There are no negative values under a square root sign
- There are no zero values in the denominator (bottom) of a fraction
Example 3
Find the domain and range of the function `f(x)=sqrt(x+2)/(x^2-9),` without using a graph.
Solution
In the numerator (top) of this fraction, we have a square root. To make sure the values under the square root are non-negative, we can only choose `x`-values grater than or equal to -2.
The denominator (bottom) has `x^2-9`, which we recognise we can write as `(x+3)(x-3)`. So our values for `x` cannot include `-3` (from the first bracket) or `3` (from the second).
We don't need to worry about the `-3` anyway, because we dcided in the first step that `x >= -2`.
So the domain for this case is `x >= -2, x != 3`, which we can write as `[-2,3)uu(3,oo)`.
To work out the range, we consider top and bottom of the fraction separately.
Numerator: If `x=-2`, the top has value `sqrt(2+2)=sqrt(0)=0`. As `x` increases value from `-2`, the top will also increase (out to infinity in both cases).
Denominator: We break this up into four portions:
When `x=-2`, the bottom is `(-2)^2-9=4-9=-5`. We have `f(-2) = 0/(-5) = 0.`
Between `x=-2` and `x=3`, `(x^2-9)` gets closer to `0`, so `f(x)` will go to `-oo` as it gets near `x=3`.
For `x>3`, when `x` is just bigger than `3`, the value of the bottom is just over `0`, so `f(x)` will be a very large positive number.
For very large `x`, the top is large, but the bottom will be much larger, so overall, the function value will be very small.
So we can conclude the range is `(-oo,0]uu(oo,0)`.
Have a look at the graph (which we draw anyway to check we are on the right track):
Show graph
We can see in the following graph that indeed, the domain is `[-2,3)uu(3,oo)` (which includes `-2`, but not `3`), and the range is "all values of `f(x)` except `F(x)=0`."
Graph of `f(x)=sqrt(x+2)/(x^2-9)`.
Summary
In general, we determine the domain by looking for those values of the independent variable (usually x) which we are allowed to use. (We have to avoid 0 on the bottom of a fraction, or negative values under the square root sign).
The range is found by finding the resulting y-values after we have substituted in the possible x-values.
Exercise 1
Find the domain and range for each of the following.
(a) `f(x) = x^2+ 2`.
Answer
Domain: The function
f(x) = x2 + 2
is defined for all real values of x (because there are no restrictions on the value of x).
Hence, the domain of `f(x)` is
"all real values of x".
Range: Since x2 is never negative, x2 + 2 is never less than `2`
Hence, the range of `f(x)` is
"all real numbers `f(x) ≥ 2`".
We can see that x can take any value in the graph, but the resulting y = f(x) values are greater than or equal to 2.
Note
- It is important to label the axes when sketching graphs. It helps with understanding what the graph represents.
- We saw how to sketch such graphs in Graph of a Function.
Need Graph Paper?
(b) `f(t)=1/(t+2)`
Answer
Domain: The function
`f(t)=1/(t+2)`
is not defined for t = -2, as this value would result in division by zero. (There would be a 0 on the bottom of the fraction.)
Hence the domain of f(t) is
"all real numbers except -2"
Range: No matter how large or small t becomes, f(t) will never be equal to zero.
[Why? If we try to solve the equation for 0, this is what happens:
`0=1/(t+2)`
Multiply both sides by (t + 2) and we get
`0 = 1`
This is impossible.]
So the range of f(t) is
"all real numbers except zero".
We can see in the graph that the function is not defined for `t = -2` and that the function (the y-values) takes all values except `0`.
(c) `g(s)=sqrt(3-s)`
Answer
The function
`g(s)=sqrt(3-s)`
is not defined for real numbers greater than 3, which would result in imaginary values for g(s).
Hence, the domain for g(s) is "all real numbers, s ≤ 3".
Also, by definition,
`g(s)=sqrt(3-s) >= 0`
Hence, the range of g(s) is "all real numbers `g(s) ≥ 0`"
We can see in the graph that s takes no values greater than 3, and that the range is greater than or equal to `0`.
(d) `f(x) = x^2+ 4` for `x > 2`
Answer
The function `f(x)` has a domain of "all real numbers, `x > 2`" as defined in the question. (There are no resulting square roots of negative numbers or divisions by zero involved here.)
To find the range:
- When `x = 2`, `f(2) = 8`
- When x increases from `2`, `f(x)` becomes larger than `8` (Try substituting in some numbers to see why.)
Hence, the range is "all real numbers, `f(x) > 8`"
Here is the graph of the function, with an open circle at `(2, 8)` indicating that the domain does not include `x = 2` and the range does not include `f(2) = 8`.
The function is part of a parabola. [See more on parabola.]
Exercise 2
More Domain and Range Examples
In case you missed it earlier, you can see more examples of domain and range in the section Inverse Trigonometric Functions.
See also Domain and Range Calculator.
We fire a ball up in the air and find the height h, in metres, as a function of time t, in seconds, is given by
h = 20t − 4.9t2
Find the domain and range for the function h(t).
Answer
Generally, negative values of time do not have any meaning. Also, we need to assume the projectile hits the ground and then stops - it does not go underground.
So we need to calculate when it is going to hit the ground. This will be when h = 0. So we solve:
20t − 4.9t2 = 0
Factoring gives:
(20 − 4.9t)t = 0
This is true when
`t = 0\ "s"`,
or
`t=20/4.9 = 4.082 text(s)`
Hence, the domain of the function h is
"all real values of t such that `0 ≤ t ≤ 4.082`"
We can see from the function expression that it is a parabola with its vertex facing up. (This makes sense if you think about throwing a ball upwards. It goes up to a certain height and then falls back down.)
What is the maximum value of h? We use the formula for maximum (or minimum) of a quadratic function.
The value of t that gives the maximum is
`t = -b/(2a) = -20/(2 xx (-4.9)) = 2.041 s `
So the maximum value is
20(2.041) − 4.9(2.041)2 = 20.408 m
By observing the function of h, we see that as t increases, h first increases to a maximum of 20.408 m, then h decreases again to zero, as expected.
Hence, the range of h is
"all real numbers, `0 ≤ h ≤ 20.408`"
Here is the graph of the function h:
Functions defined by coordinates
Sometimes we don't have continuous functions. What do we do in this case? Let's look at an example.
Exercise 3
Find the domain and range of the function defined by the coordinates:
`{(−4, 1), (−2, 2.5), (2, −1), (3, 2)}`
Answer
The domain is simply the x-values given: `x = {−4, −2, 2, 3}`
The range consists of the `f(x)`-values given: `f(x) = {−1, 1, 2, 2.5}`
Here is the graph of our discontinuous function.