Introduction to Geometry

Basic Geometry Worksheet

Download this Basic Geometry Worksheet with 10 questions and answers as a practice test.

Introduction to Geometry Worksheet with Answers

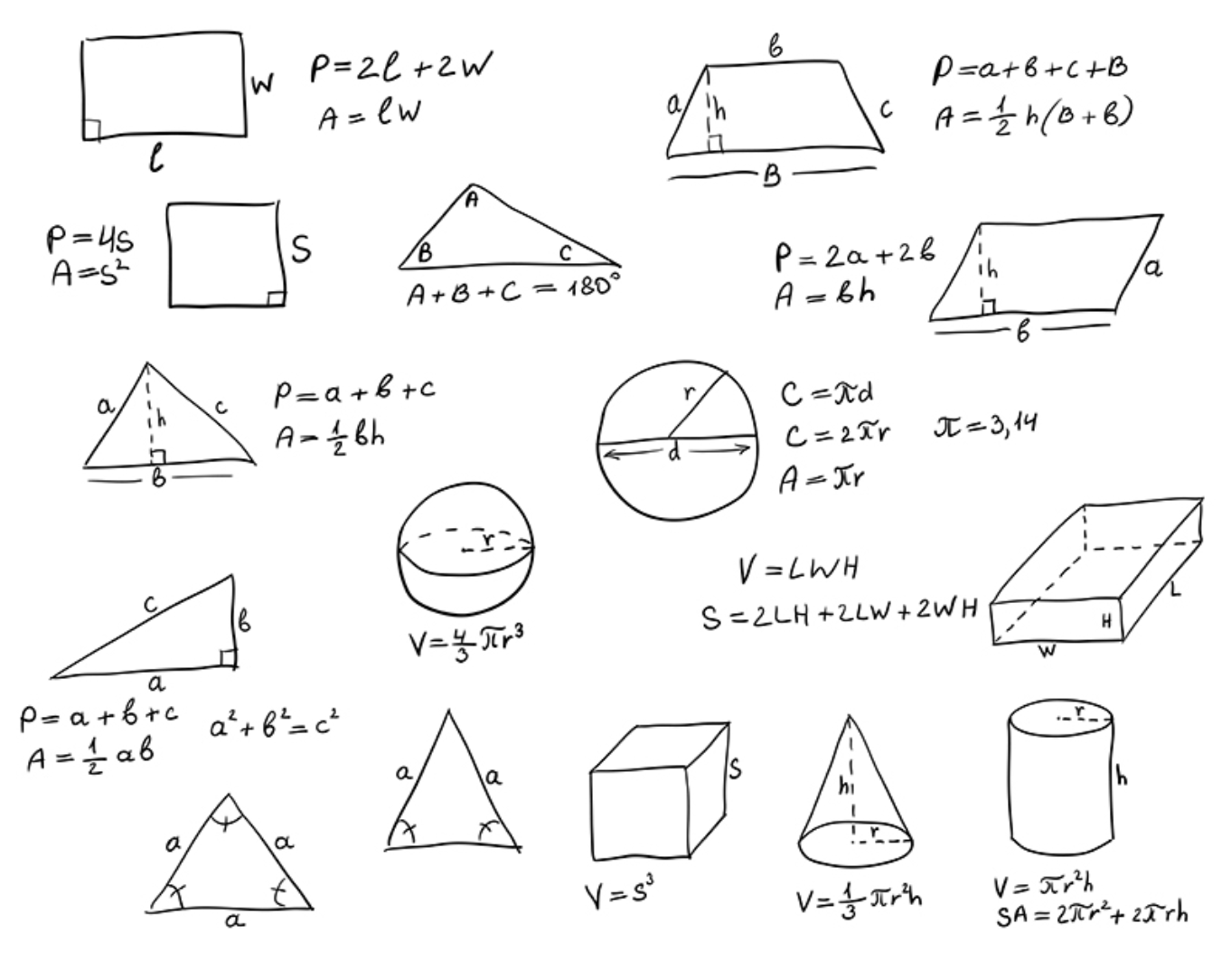
Geometry has allowed humanity to greatly expand our understanding of the objects around us, and it is used on a daily basis not only in mathematics but in many branches of science. Innumerable industries rely on geometric principles, including construction, building design, product development, and city planning. Follow along as we give you an introduction to geometry, helping you see the world from a new angle.

What is Geometry?

Geometry is a field of mathematics that relates to objects, or geometric shapes as they are referred to, and their sizes, shapes, positions, or spacial properties. This subject generally covers the following areas:

• Distances
• Angles and Shapes
• Patterns
• Area and Perimeter
• Circumference and Volume

These, along with any other visually and spatially related concepts are considered to be a part of geometry. Within the vast world of geometry, there are two principal categories.

• Euclidean
• Non-Euclidean

Euclidean Geometry

Geometry has been used since the time of the Ancient Greeks. The term "Geometry" even has Greek roots, from the Greek word “geo”, meaning earth, and “metrein” which translates to “to measure.” So it comes as no surprise that the father of Geometry is the Greek mathematician, Euclid. He even has a branch of geometry named after him—Euclidean geometry.

This is generally the first category of geometry you learn in school. That's because it explains basic geometric principles. Euclidean geometry established the foundation for much of what we understand about the field today. Academically, Euclidean geometry refers to the study of flat shapes and flat surfaces.

Non-Euclidean Geometry

There are two other major branches of geometry that are considered non-Euclidean. Non-Euclidean geometry is a rethinking of the properties of lines, points, and shapes. In other words, Euclidean geometry deals with objects on a flat plane, whereas non-Euclidean geometry deals with our world (and non-flat surfaces).

The two main kinds of non-Euclidean geometry are below.

1. Spherical Geometry Explained

Spherical geometry is the study of geometry not on a plane, but rather on a sphere. In spherical geometry, like Euclidean geometry, lines are defined as the shortest distance between two points. However, spherical geometry has no parallel lines. Triangles in spherical geometry also add up to more than 180 degrees. Spherical geometry also introduces new terms:

• A “line” between two points on a sphere is referred to as a “great circle”
• The shortest point between two points on the surface of a sphere is indicated by the arc of the great circle passing between them.

2. Hyperbolic Geometry Explained

A third major kind of geometry is hyperbolic. Hyperbolic geometry is defined as geometry on a curved surface. In hyperbolic geometry, one of the Euclidean postulates is replaced. In hyperbolic geometry, parallel lines will become further and further apart. And triangles will have angles that are less than 180 degrees in total.

Quick Guide to Euclidean Geometry

Euclidean Principles

Euclidean geometry is also sometimes referred to as “plane geometry” because it concerns flat objects. Some key properties of Euclidean geometry are:

• The shortest distance between any two points is a straight line.
• Two parallel lines will be infinitely parallel and never intersect.
• The interior angles of a triangle will add up to 180 degrees.
• Right triangles have two perpendicular sides measuring 90 degrees forming a right angle within the triangle.
• Solid shapes have a size, position, and shape that can be moved from place to place.
• Euclidean geometry is the study of planes and solid objects.

Overall, this means Euclidean geometry will be concerned with angles, triangles, squares, lines, points, and more.

Euclid’s Postulates

Euclidean geometry is centered around five postulates. These important building blocks are as follows:

• A line extends indefinitely in both directions.
• All right angles are equal to one another.
• A line segment is drawn from any one point to another
• Any two straight lines that are an equal distance from each other at two points are parallel
• A circle can be described with any point and its radius.

Euclid’s Axioms

Euclid’s axioms are still an important part of geometry today. Though they may not be mathematically proven, they're widely accepted by modern mathematicians:

• Things that are equal to the same thing are equal to each other
• If equals and equals are added, the wholes are equal
• If equals are subtracted from equals, the remainders will be equal
• Things which coincide are equal to one another
• The whole is greater than the part
• Things that are double of the same thing are equal to each other
• Things that are halves of the same thing are equal to one another

5 Types of Euclidean Geometry

1. Plane Geometry

For the purpose of plane geometry, consider that lines, points, and angles are all placed on a two-dimensional plane that goes on infinitely in all directions (while remaining flat). Understanding the concepts and study of plane geometry is essential in order to understand more complex forms of geometry. Some important terms to know are:

• A given point on a plane that is indicated with a set of coordinates
• Collinear points are points along the same line
• A line is infinite in two directions along the plane
• A line segment has a starting and ending point
• A ray has a starting point and then goes on infinitely in one direction
• Parallel means infinitely parallel. If two lines do not intersect anywhere on a plane, they are parallel
• Perpendicular lines are those that intersect at a right angle

Plane Geometry - Angles

If two lines are not parallel, they will intersect at some point. When they intersect, the two lines form an angle, typically measured in degrees. There are generally considered to be four kinds of angles:

• A straight angle is exactly 180 degrees
• A right angle is exactly 90 degrees
• An obtuse angle is greater than 90 degrees, but less than 180
• An acute angle is less than 90 degrees

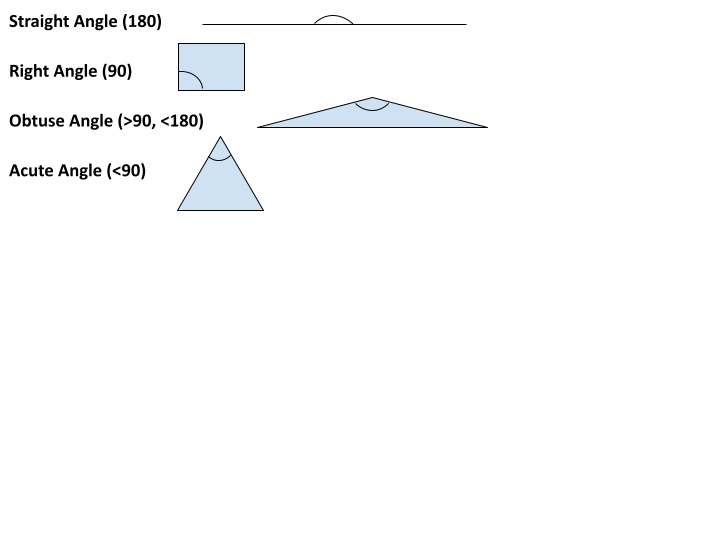
Angles can also be either complementary or supplementary. If the sum of two angles is 180 degrees, they are considered to be supplementary angles. If the sum is 90 degrees, they are instead considered to be supplementary.

Plane Geometry - Shapes

Shapes in plane geometry are classified by their properties. These are all two-dimensional shapes and can be placed on a flat plane. In order to be considered a polygon, shapes must have more than two lines and be closed. Some of the most commonly seen plane shapes include:

• Triangles (three sides, three vertices)
• Quadrilaterals (four sides, four vertices)

There are three kinds of triangles.

1. Equilateral triangles have three equal sides and angles.
2. A scalene triangle has three unequal sides and angles.
3. An isosceles triangle has only two equal sides.

When studying triangles in particular, there are a number of theorems to help identify their properties. These include the Pythagorean Theorem, the angle sum property, the exterior angle theorem, and more. Triangles can be fully graphed with only two points and angles. For quadrilaterals, triangles, and all other polygons, it is also important to understand the concept of symmetry. Symmetry is when an object can have a line drawn through it and be exactly the same on both sides. As an example, a circle has infinite lines of symmetry.

2. Solid Geometry

Solid geometry is concerned with objects and solid figures that are three-dimensional. This can include the following shapes, among others:

• Cylinder
• Cube
• Sphere
• Cone
• Prism
• Pyramid
• Cuboids

In order to be considered three-dimensional, an object needs to have length, width, and height. These three-dimensional shapes are classified by faces, edges, and vertices. Vertices are the corners of the shapes, faces are the sides, and edges are the lines. For example, a cube has a total of 8 vertices, while a cone only has one single vertex.

3. Geometric Measurement

When measuring objects in geometry, there are many things to consider. Every geometric shape can be measured in perimeter, area, surface area, and volume.

• Perimeter is the distance around the outside of plane (two-dimensional) shapes
• Area is the amount of space occupied by a shape
• Volume is the area within a shape
• A solid's surface area is the area of all of the shape's faces

These measurements can be calculated in different ways, using specific formulas dependent on the nature of the shape.

4. Coordinate Geometry

Coordinate geometry, also referred to as Analytic Geometry, identifies a point on a plane with a set of ordered numbers, (X, Y). This set of numbers (coordinates) can be plotted on a graph, a coordinate plane, along with other coordinates to indicate a particular shape. In coordinate geometry, the plane is divided into four quadrants. The top right quadrant will have two positive coordinates, while the bottom left will have two negative coordinates.

Any coordinate to the left of the y-axis will be negative, while those on the right will be positive. Conversely, any coordinate above the x-axis will be positive, while those below it will be negative. This is called a Cartesian coordinate system.

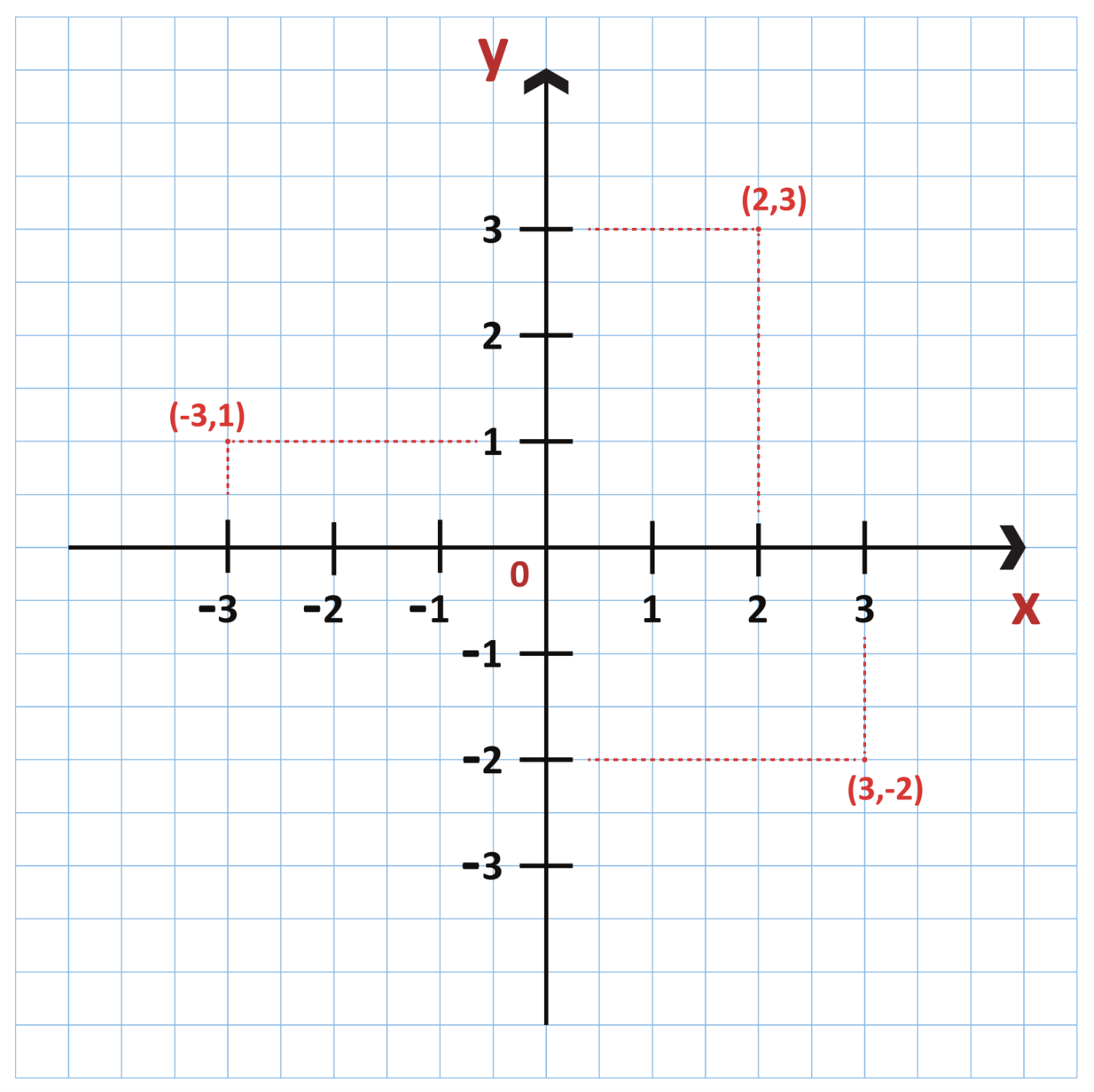
Coordinate geometry can show properties of geometric figures, such as lines, curves, ellipses, hyperbolas, circles, and more. Curves are represented with an algebraic equation. With the use of many different formulas, including the distance formulas, the section formula, the midpoint formula, and more, these shapes can be completely graphed and identified. In other words, an algebraic equation can indicate a specific curve.

Three-Dimensional Coordinate Geometry

Logically, as a two-dimensional plane shape has two-digit coordinates, three-dimensional objects have three. Instead of (X, Y), these coordinates are indicated with (X, Y, Z). It has all of the concepts from two-dimensional coordinate geometry, and more.

The three-dimensional Cartesian coordinate system instead has three axes. The X, Y, and Z-axis are all perpendicular to one another. Since there are three axes instead of two, that means that instead of quadrants, these graphs are divided into a total of eight sections (sometimes called octants). The coordinates are called:

• Abscissa is the first coordinate and indicates the distances from the origin along the x-axis
• Ordinate is the second coordinate, and is the perpendicular distance of the point from the x-axis. It is parallel to the y-axis
• Applicate is the third coordinate, the distance from the z-axis

Together, these three coordinates are like directions to find a given point in space. Any point in three-dimensional coordinate geometry can be indicated with three coordinates (X, Y, Z). This is one of two ways to represent a point in three-dimensional geometry and the properties of space, referred to as the Cartesian form. The Cartesian form can be used to represent any three-dimensional shape in geometry. The other way to represent a point, line of shape is called the vector form.

5. Differential Geometry

Differential geometry is the speciality of non-euclidean geometry that combines differential calculus with geometric principles. It’s used to study surfaces, manifolds, and curves within space. Differential geometry can is used in numerous fields including:

• GPS
• Geometric controls in robotics
• Image Analytics
• Animation
• Medical Imaging
• Computer vision (AI)
• String Theory

Perhaps the easiest way to think about this is to imagine a screw. A screw has a solid shaft in the middle surrounded by the helical thread. The thread allows the screw to pull itself into another material. Because the thread is not on a singular plane, you can’t get an accurate measurement for the radius without understanding how the curvature of curves and surfaces work.

Understanding these allows for the shortest path between two points on a surface to be measured.

Geometric Formulas

The distance formula helps find the shortest distance between two points. It is calculated by using the following formula. The distance equals the square root of (x1- x2) squared + (y2-y1) squared +(z1-z1) squared). This formula can help you ascertain any missing coordinates.

The mid-point formula is a new point. The abscissa is the average of the x values of the given points, while the ordinate is the average of the y values of the two points that were given. The midpoint is on the line joining two points as is located in the exact middle of the two points.

Section formula can help you find the coordinates of a point that divides the line segment. The point which divides the given two points is on the line adjoining the two points. It is available either between the two points or on the line beyond the points indicated. The formula is used widely in Physics as well as Mathematics. In Physics, it is used to find the center of mass and points of equilibrium.

Geometric Terminology

Some of the key vocabulary words that are important for a geometry student to know and understand are below:

• Diameter - A straight line passing through the center of a circle (or sphere) and reaching the other end
• Ray - A line segment that goes on infinitely in one direction
• Parallel - Two lines that do not intersect
• Vertex (vertices) - the intersection point of two sides of a plane figure
• Face - Any of the individual flat surfaces of a solid object
• Edge - Any line segment joining one vertex to another
• Perpendicular - when two lines (or line segments) intersect at a 90-degree angle
• Vector - A line that shows magnitude and direction. Often used to represent distance or acceleration
• Transversal - A line intersecting two or more given lines in a plane at different points
• Complementary angles - when the sum of two angles is exactly 90 degrees
• Supplementary angles - when the sum of two angles is exactly 180 degrees
• Plane - A flat surface that extends infinitely in all directions (2-dimensional)

10 Basic Geometry Practice Problems

1. What is the volume of a pyramid whose base is a regular pentagon with an area of 60 m² and whose height is 10 m?

Answer

2. What is the value of F + V - E for a prism whose cross-section is a heptagon?

Answer

3. A torus has the following values R = 15 m and r = 4 m. What is the volume of the torus?

Answer

4. AB is an arc of length 14 in. on the circumference of a circle with center C. The size of angle ACB is 3.5 radians. Find the radius of the circle.

Arc Length Formula: L = θ × r

Variables:

(Arc length) L = 14 in.

(Angle ACB) θ = 3.5 radians

(Radius) r = ?

Answer

5. BC is an arc with a length of 72 feet on the circumference of a circle with the center D and a diameter of 24 feet. What is the size of the angle BDC in radians?

Answer

6. Convert 2𝞹/4 radians to degrees.

Answer

7. The following isosceles triangle has two equal sides, each with a length of 10.3. Angle A is a right angle. What is the size of the missing angle "B"?

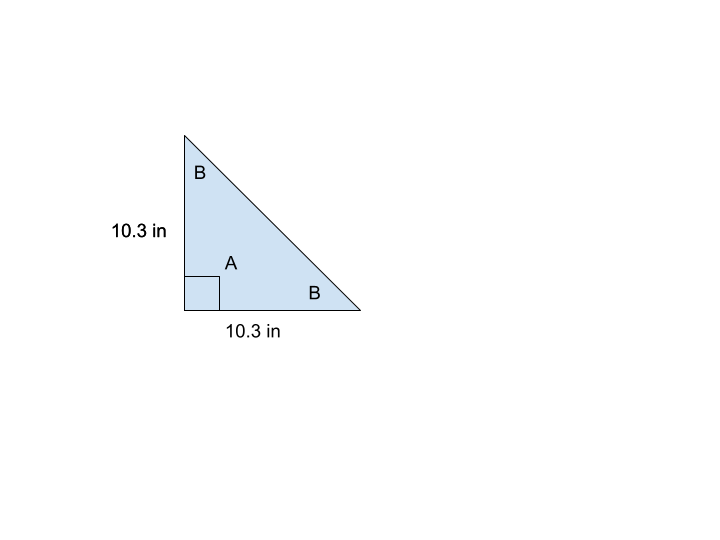
Answer

8. Find the side length of a parallelogram with perimeter of 22 in. and base of 8.3 in.?

Parallelogram Perimeter Formula:

P = 2(b + s)

Variables:

(Perimeter) P = 22

(Base) b = 8.3

(Side) s = ?

Answer

9. In the following diagram, what is the size of angle BAC?

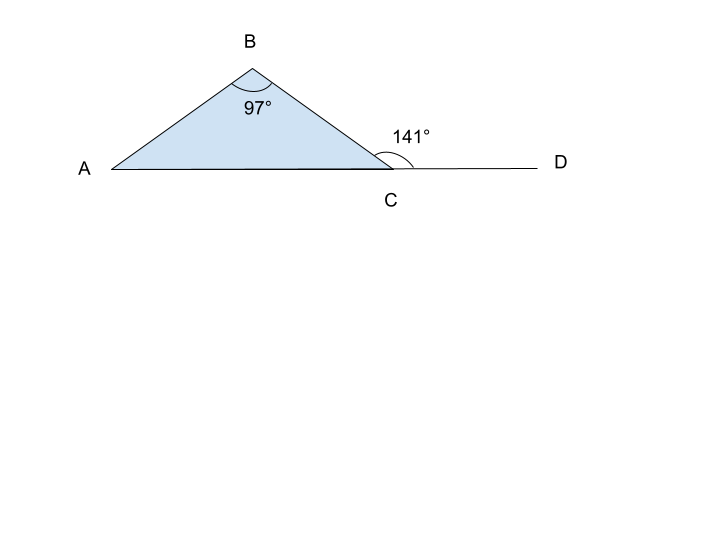
Exterior Angle Theorem: ∠BAC = ∠BCD − ∠ABC

Answer

10. What is the surface area for a regular tetrahedron when the total length of the edges is 48 mm? Round to the nearest 1/100th

Answer