Kite vs Rhombus in Geometry
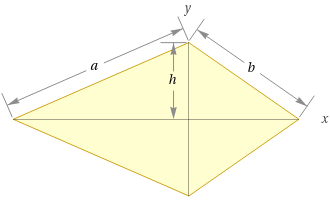
What is a Kite Shape?
A kite shape is a type of quadrilateral, which means it has four sides. It's a two-dimensional shape, meaning width and length, but no depth. It has two pairs of adjacent sides that are not equal in length, and one pair of opposite sides that are equal in length. All four angles in the kite shape are also equal.What is a Rhombus Shape?
A rhombus shape is also a type of quadrilateral. It is a two-dimensional shape that has four sides of equal length and four angles that are also equal. The diagonals of a rhombus intersect at 90 degree angles, and it is also a type of parallelogram.How Kite and Rhombus Differ?
The main difference between a kite and a rhombus is the length of their sides. A rhombus has four sides of equal length, while a kite has two sides of equal length and two sides of different length. A rhombus is also a type of parallelogram, while a kite is not.Properties of Kite and Rhombus
Both the kite and rhombus are quadrilaterals, meaning they have four sides. Both shapes have four angles that are equal in measure. Both shapes also have two pairs of adjacent sides that are equal in length and two pairs of opposite sides that are equal in length.Using Kite and Rhombus in Geometry
Kites and rhombuses can be used in geometry to solve many problems. These shapes are often used to prove theorems, as they can be used to construct other shapes. They can also be used to measure angles and lengths, and to calculate areas and perimeters.Practice Problems
1. Which of the following is true about kites?
A. They have four angles of equal measure.
B. They have two pairs of adjacent sides of equal length.
C. They are types of parallelograms.
D. All of the above.
Answer: D. All of the above.
2. What is the difference between kites and rhombuses?
A. Kites have four sides of equal length, while rhombuses have two.
B. Kites are types of parallelograms, while rhombuses are not.
C. Kites have four angles of equal measure, while rhombuses do not.
D. Kites have two pairs of opposite sides of equal length, while rhombuses do not.
Answer: B. Kites are types of parallelograms, while rhombuses are not.
3. What is the measurement of the angles in a rhombus?
Answer: The angles in a rhombus are all equal in measure.
4. What is the formula for finding the area of a kite?
Answer: The formula for finding the area of a kite is A = � * d1 * d2, where d1 and d2 are the lengths of the diagonals.
5. What is the perimeter of a rhombus with sides of length 8?
Answer: The perimeter of a rhombus with sides of length 8 is 32.
6. What is the measure of the angles in a kite?
Answer: The angles in a kite are all equal in measure.
7. What is the formula for finding the perimeter of a rhombus?
Answer: The formula for finding the perimeter of a rhombus is P = 4 * s, where s is the length of one side.
8. What is the area of a kite with diagonals of length 8 and 10?
Answer: The area of a kite with diagonals of length 8 and 10 is 40.
9. What is the measure of the angles in a parallelogram?
Answer: The angles in a parallelogram are not necessarily equal in measure.
10. What is the formula for finding the area of a rhombus?
Answer: The formula for finding the area of a rhombus is A = � * d1 * d2, where d1 and d2 are the lengths of the diagonals.
Summary of the Lesson
In this lesson, we discussed the differences between kites and rhombuses in geometry. We discussed the properties of each shape, as well as how they can be used in geometry. Finally, we went through some practice problems to test our understanding. Kites and rhombuses are both important shapes in geometry and can be used to solve many problems.FAQ
What is the difference between a kite and a rhombus?
The primary difference between a kite and a rhombus is that a kite has two pairs of adjacent sides that are of different lengths, while a rhombus has all four sides of equal length. Additionally, the angles of a kite are not necessarily all equal, while the angles of a rhombus are all equal.