Conic Sections Review

A conic section is a curve that can be formed by intersecting a cone with a plane. There are four types of conic sections: circles, ellipses, parabolas, and hyperbolas. In this review, we'll take a look at each type of conic section and how it can be formed.

Circles

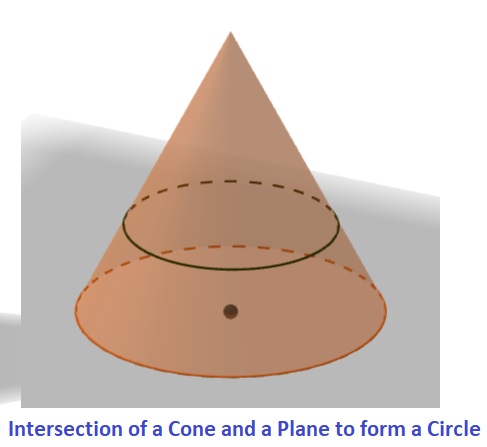
A circle is the set of all points in a plane that are equidistant from a given point called the center. A circle can be formed by intersecting a cone with a plane that is parallel to the base of the cone. The figure below shows how a circle can be formed in this way.

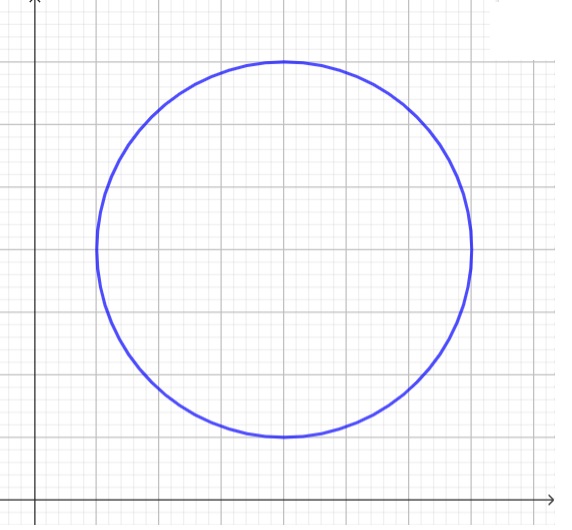
The graph of a circle in the coordinate plane is given as shown below:

Ellipses

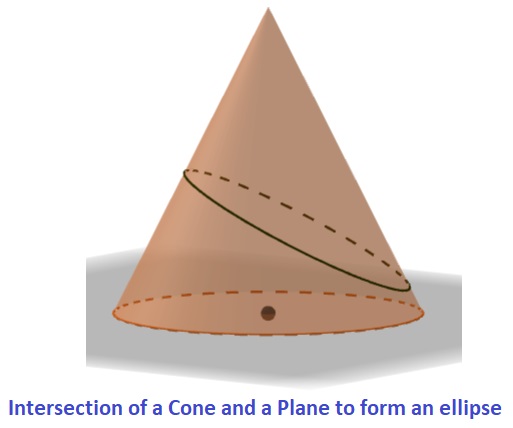
An ellipse is the set of all points in a plane such that the sum of the distances from two fixed points (foci) is constant. An ellipse can be formed by intersecting a cone with a plane that is not parallel to the base or the apex of the cone. The figure below shows how an ellipse can be formed in this way.

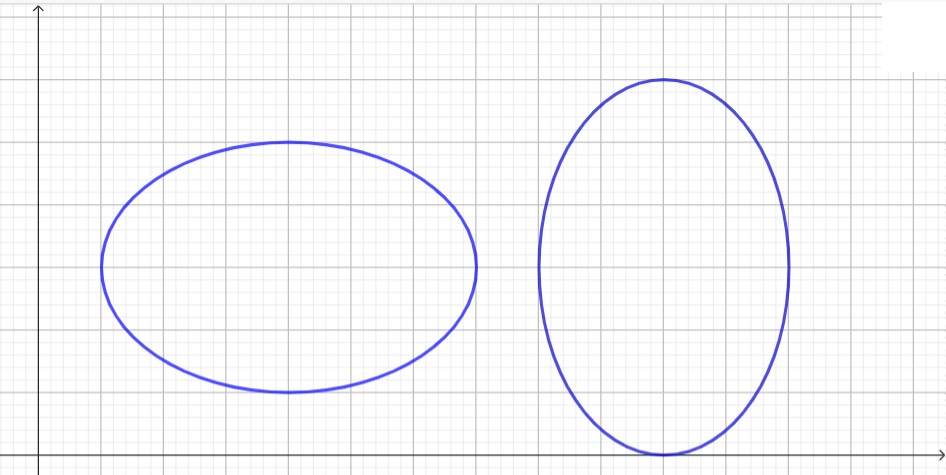
The graph of two different types of ellipse in the coordinate plane is given as shown below:

Parabolas

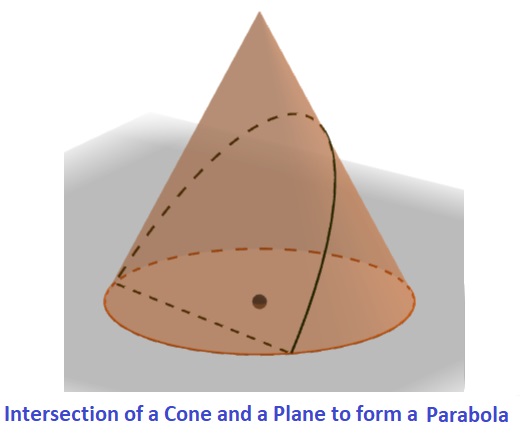
A parabola is the set of all points in a plane such that the distance from a fixed point (focus) is equal to the distance from a fixed line (directrix) squared. A parabola can be formed by intersecting a cone with a plane that is perpendicular to the axis of the cone and passes through its apex. The figure below shows how a parabola can be formed in this way.

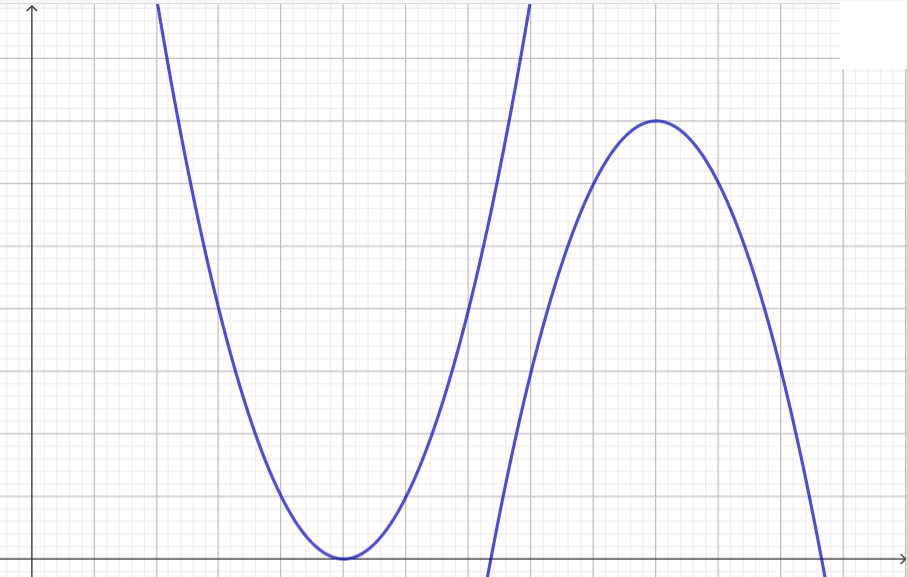
The graph of parabolas that opens (i)upwards and (ii)downwards in the coordinate plane is given as shown below:

Hyperbolas

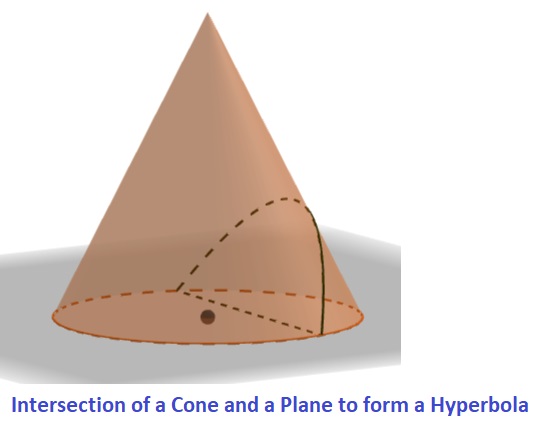
A hyperbola is the set of all points in a plane such that the difference between the distances from two fixed points (foci) is constant. A hyperbola can be formed by intersecting a cone with a plane that is not parallel or perpendicular to either the base or apex of the cone as shown in the figure below.

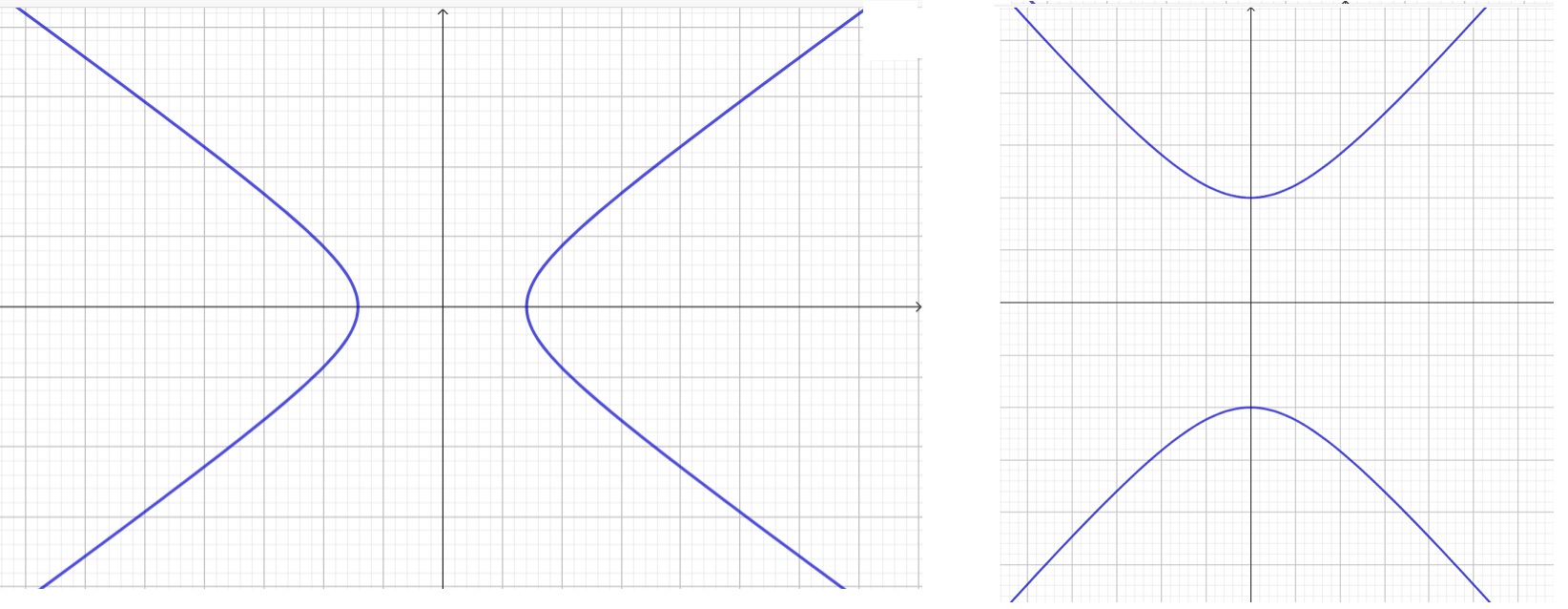
The graph of a hyperbola in the coordinate plane is given as shown below:

Conclusion:

In conclusion, there are four types of conic sections: circles, ellipses, parabolas, and hyperbolas which can be generated by intersectional planes and cones under specific circumstances as we explored in this review! We hope you found this helpful and good luck on your test!

FAQ

What is the 4 types of conic sections geometry?

There are four types of conic sections: circles, ellipses, parabolas, and hyperbolas. Each type can be generated by intersecting a cone with a plane under specific circumstances.

Why is it called conic sections?

Conic sections are named after the cone, because a cone can be used to generate each type of curve.

How are the 4 conic sections formed?

The four types of conic sections can be formed by intersecting a cone with a plane. The type of curve that is generated depends on the angle of intersection between the plane and the cone.