The Angles of a Square

A square is a four-sided regular polygon with each of its interior angles having a measure of 90 degrees. In a regular polygon, all the side lengths are equal, therefore, we can say that a square is a quadrilateral with all sides having an equal length. Examples of objects around us that can be in the form of a square are chessboard, stamps, paper napkins, etc. The basic figure of a square is shown below.

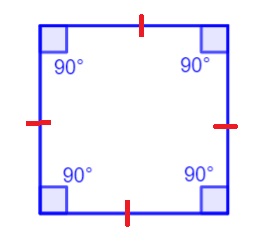
In this article, we want to learn about the properties of a square, its area, perimeter and the length of its diagonal.

Definition

A square is a quadrilateral in which:

• The opposite side lengths are parallel.
• The four sides are equal.
• The four interior angles have a measure of 90°.

Properties of a Square

Some of the properties of a square are given below.

• A square is a quadrilateral which has 4 sides and 4 vertices.
• The four sides of the square are equal to each other.
• The opposite sides of a square are parallel to each other.
• The adjacent sides are perpendicular to one another.
• The interior angle of a square at each vertex is 90°.
• The sum of all interior angles and exterior angles is both 360° respectively.
• The diagonals are of equal lengths, bisects each other and are perpendicular to one another.

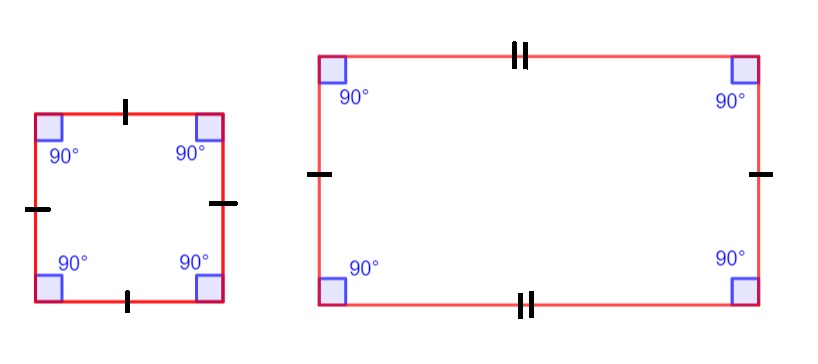
Squares Versus Rectangles

The major difference between a square and rectangle is in the side lengths. In a square, all the sides are equal in length whereas in a rectangle, the opposite sides are equal in lengths and parallel to one another.

Area of a Square

The area of any figure is the space occupied by the figure. For example, the area of a floor is the space which the floor occupies. 

Given a square with side length, s, the area is calculated using the formula:

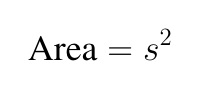
The unit for area is always in square units like cm², m², km², etc. The unit being squared depends on the unit of the side length.

Perimeter of a Square

The perimeter of any figure is the total length of the boundary of the figure. Consider the square below:

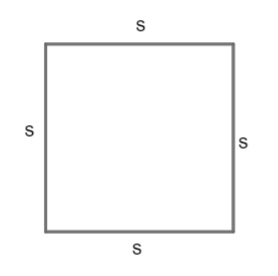
Add the length of all the sides. 

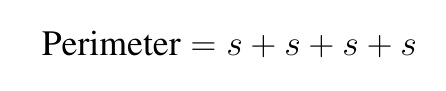
Therefore, the perimeter of a square with side length s is calculated using the formula:

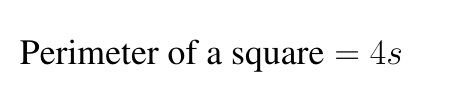
The perimeter is expressed in linear units like cm, m, km, and so on.

Diagonals of a Square

The diagonal of a square is a line segment that joins any two of its non-adjacent vertices. 

In the square PQRS below, PR and QS are the diagonals of the square. As stated in the property, the diagonals PR and QS are of equal lengths.

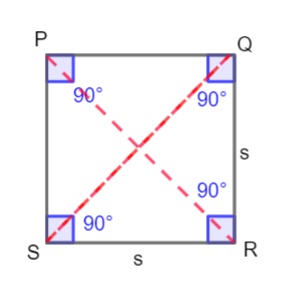
Each diagonal cuts the square into two equal right triangles where each diagonal forms the hypotenuse of the right-angled triangles formed.

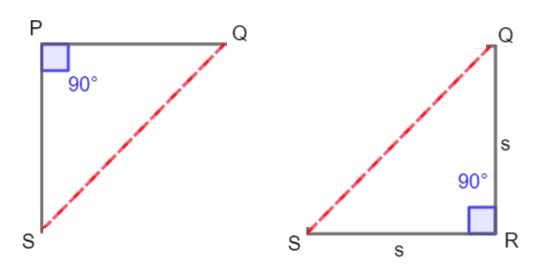
Thus, for a square with side length S, we can find the length of the diagonal using the Pythagorean theorem:

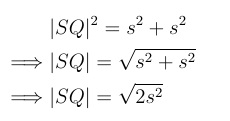
Thus, the length of the diagonal of a square with side length is calculated using the formula:

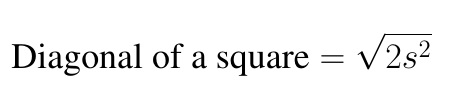
Conclusion

We have discussed the properties of a square, the area, perimeter and how to find the length of its diagonal. You can find the area and perimeter using the side length of the square. In addition, whatever measure is given (area, perimeter, diagonal length), we can also find the side length of the square from it using the appropriate formula in order to carry out any required calculation.