Understanding Midpoint in Geometry
What is Midpoint?
Midpoint is an important concept in geometry, used to describe the halfway point between two points on a line, plane, or triangle. Midpoint is also known as a centroid, and is used to calculate the distance between two points. With midpoint, you can easily calculate the area of a triangle, the length of a line, or the perimeter of a plane.
Midpoint is derived from the Greek words "mid" and "point," literally meaning the middle point. It is a common geometrical concept in mathematics, used to measure distances, angles, and other properties of shapes. Midpoint is also used to determine the center of a circle, the center of a triangle, or the center of a polygon.
Geometric Midpoint
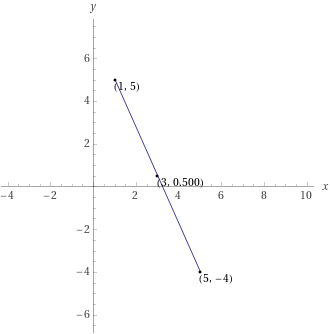
A geometric midpoint is the point that lies halfway between two other points on a line, plane, or triangle. It is usually represented by a dot on a graph, and is used to calculate the distance between two points. The midpoint of a line is the point that divides the line into two equal parts. The midpoint of a triangle is the point at which all three sides of the triangle meet.
In order to calculate the midpoint of a line, the midpoint formula is used. The formula for the midpoint of a line is: M=(x1+x2)/2, where x1 and x2 are the x-coordinates of the two points on the line. The y-coordinate of the midpoint is calculated in a similar way: M=(y1+y2)/2.
Midpoint Theorem
The midpoint theorem states that the midpoint of a line is the point at which the line is divided into two equal parts. The midpoint theorem can be used to calculate the length of a line, the area of a triangle, or the perimeter of a plane. The midpoint theorem is also used to calculate the center of a circle, the center of a triangle, or the center of a polygon.
The midpoint theorem can be used to calculate the length of a line segment by using the midpoint formula. The formula for the length of a line segment is: L=v((x1-x2)2 + (y1-y2)2), where x1 and x2 are the x-coordinates of the two points on the line and y1 and y2 are the y-coordinates of the two points on the line.
Midpoint of a Triangle
The midpoint of a triangle is the point at which all three sides of the triangle meet. The midpoint of a triangle can be used to calculate the area of a triangle, the perimeter of a triangle, or the center of a triangle. The formula for the area of a triangle is: A=1/2ah, where a is the length of one side of the triangle and h is the height of the triangle. The formula for the perimeter of a triangle is: P=a+b+c, where a, b, and c are the lengths of the sides of the triangle. The formula for the center of a triangle is: C=(x1+x2+x3)/3, where x1, x2, and x3 are the x-coordinates of the three points of the triangle.
Practice Problems
1. Find the midpoint of the line segment with endpoints (2,3) and (7,9)
Answer: (4.5, 6)
2. Find the length of the line segment with endpoints (5,4) and (1,7)
Answer: 5.8
3. Find the area of a triangle with sides of length 5, 6, and 7
Answer: 14.7
4. Find the perimeter of a triangle with vertices (2,3), (7,9), and (4,7)
Answer: 18
5. Find the center of a triangle with vertices (1,2), (3,4), and (5,6)
Answer: (3, 4)
Summary
Midpoint is an important concept in geometry, used to describe the halfway point between two points on a line, plane, or triangle. A geometric midpoint is the point that lies halfway between two other points on a line, plane, or triangle. The midpoint theorem states that the midpoint of a line is the point at which the line is divided into two equal parts. The midpoint of a triangle is the point at which all three sides of the triangle meet. The midpoint theorem can be used to calculate the length of a line, the area of a triangle, or the perimeter of a plane. The midpoint formula is used to calculate the midpoint of a line and the midpoint theorem can be used to calculate the length of a line segment, the area of a triangle, the perimeter of a triangle, or the center of a triangle.
FAQ
What is a midpoint?
In geometry, the midpoint is the point that is halfway between two other points on a line segment.
How is a midpoint determined?
A midpoint is determined by taking the average of the x-coordinates and the average of the y-coordinates of the two points that make up the line segment.
What is the formula for finding the midpoint?
The formula for finding the midpoint is as follows: Midpoint = (x1 + x2) / 2, (y1 + y2) / 2.