Internal Division of a Line Segment

In geometry, there are two types of division of a line- external and internal. External division is when the point that divides the line segment lies outside the coordinates of the line segment while internal division is when the point that divides the line segment lies in between the coordinates of the line segment. In this post, we will focus on internal division. 

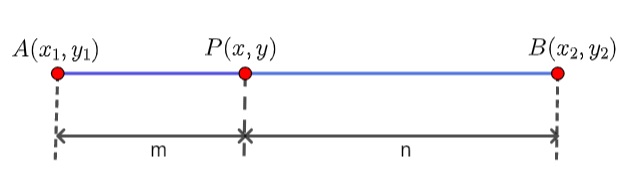
Consider the line segment AB with endpoints A(x1,y1) and B(x2,y2). If a point P divides segment AB in the ratio m:n, then the coordinates of point P can be calculated using the formula:

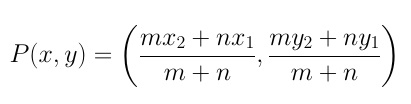
Example:: The point K divides segment RS with endpoints R(-4, 3) and S(9,4) in the ratio 4:6, find the coordinates of point K.

Solution:

In this case: m:n=4:6, (x1,y1)=R(-4, 3) and (x2,y2)=S(9,4).

Substitute these values into the formula for internal section division.

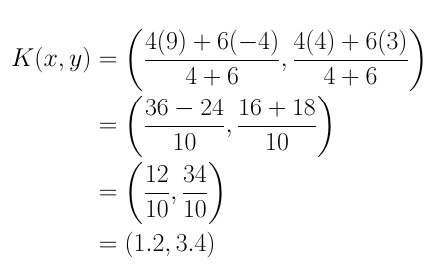
The coordinates of point K that divides RS in the ratio 4:6 is (1.2, 3.4).

Special Cases of the Internal Section Formula

There are two special cases when it comes to internal division of a line segment. 

Case 1 (m=k and n=1)

In a case where the ratio m:n=k:1, the formula above is modified and given in the form below:

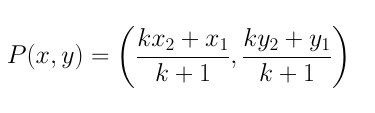
Example: The point P divides segment AB with endpoints A(2, -2) and B(5,9) in the ratio 4:1, find the coordinates of point P.

Solution:

In this case: k=4, (x1,y1)=A(2, -2) and (x2,y2)=B(5,9).

Substitute these values into the modified formula for internal section division.

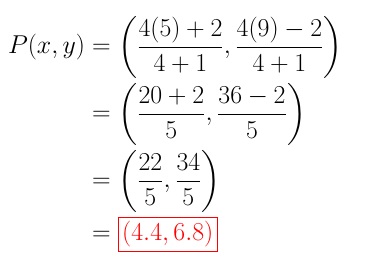
 The coordinates of point P that divides AB in the ratio 4:1 is (4.4, 6.8).

Case 2 (m=n)

In a case where the ratio m = n, the internal section formula is modified as follows:

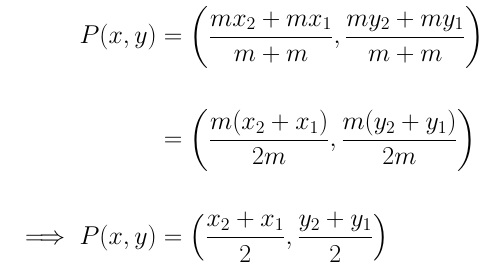
The form obtained when m=n is referred to as the midpoint formula.

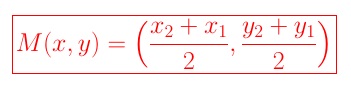
Example: The endpoint of segments PQ are P(2, 0) and Q(8,15), find the coordinates of the midpoint of PQ.

Solution:

In this case: (x1,y1)=P(2, 0) and (x2,y2)=Q(8,15).

Substitute these values into the midpoint formula:

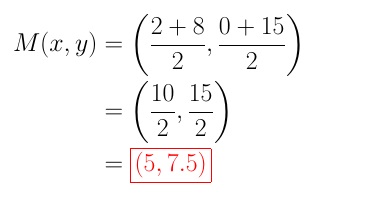
The coordinates of the midpoint of PQ is at (5, 7.5). 

FAQ

What is internal division and external division?

In geometry, there are two types of division - external and internal. External division is when the point lies outside while internal division is when the point lies in between the coordinates of the line segment.

 How do you prove internal division?

The most important thing to remember is that the line/point must be in between the endpoints.

 What is the meaning of external division?

External division is when a line or curve intersects a figure into two parts.