What are Spherical Coordinates?

Introduction to 3D Coordinates

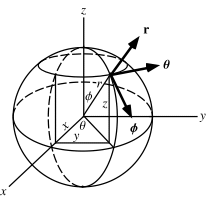
Spherical coordinates are an extension of the two-dimensional Cartesian coordinate system, which is used to represent points in Euclidean geometry. Instead of two axes, spherical coordinates use three axes to represent a 3D point in space. These three axes are known as the polar, azimuthal, and radial axes. Together, these three axes form the spherical coordinate system.

The polar axis is a line that passes through the origin and is perpendicular to the plane of the two other axes. The azimuthal axis lies in the plane of the two other axes and passes through the origin. The radial axis is the line that passes through the origin and is perpendicular to the plane of the two other axes.

Calculating Spherical Coordinates

The spherical coordinate system uses three angles and one length to locate any point in space. The angles are the polar angle, ?, the azimuthal angle, f, and the radial angle, ?. The length is the distance, or radius, r. The equations for calculating spherical coordinates are as follows:

• r = sqrt(x^2 + y^2 + z^2)
• ? = arctan (y/x)
• f = arctan (sqrt(x^2+y^2)/z)
• ? = sqrt(x^2 + y^2 + z^2) * sin(?)

The values of x, y, and z can be calculated from the polar, azimuthal, and radial angles using the following equations:

• x = r * sin(?) * cos(f)
• y = r * sin(?) * sin(f)
• z = r * cos(?)

Applications of Spherical Coordinates

Spherical coordinates are used in a variety of applications, including navigation, physics, astronomy, and engineering. One of the most common applications of this system is in spherical trigonometry, which is used to calculate distances, angles, and areas on the surface of a sphere. Spherical coordinates are also used in astronomy to describe the position of stars relative to Earth.

In addition to these applications, spherical coordinates can also be used to solve problems involving 3D shapes, such as cylinders, cones, and spheres. By using the three angles and the radius, a point in space can be precisely located. This makes it possible to calculate the surface area and volume of different 3D shapes.

Examples of Spherical Coordinates

To better understand spherical coordinates, let's look at a few examples. In the first example, we'll calculate the spherical coordinates of the point (3, 4, 5). To do this, we'll use the equations we learned earlier. First, we'll calculate the radius:

r = sqrt(3^2 + 4^2 + 5^2)
r = sqrt(36 + 16 + 25)
r = sqrt(77)
r = 8.77

Next, we'll calculate the polar angle:

? = arctan (4/3)
? = arctan (1.33)
? = 53.13�

Finally, we'll calculate the azimuthal angle:

f = arctan (sqrt(3^2+4^2)/5)
f = arctan (5/5)
f = 45�

So, the spherical coordinates of the point (3, 4, 5) are (8.77, 53.13�, 45�).

Practice Problems

Let's practice calculating spherical coordinates with a few more examples.

• Calculate the spherical coordinates of the point (2, 3, 5):

  r = sqrt(2^2 + 3^2 + 5^2)
  r = sqrt(4 + 9 + 25)
  r = sqrt(38)
  r = 6.16

  ? = arctan (3/2)
  ? = arctan (1.5)
  ? = 56.31�

  f = arctan (sqrt(2^2+3^2)/5)
  f = arctan (3.6/5)
  f = 54.74�

  So, the spherical coordinates of the point (2, 3, 5) are (6.16, 56.31�, 54.74�).

• Calculate the spherical coordinates of the point (3, -4, 5):

  r = sqrt(3^2 + (-4)^2 + 5^2)
  r = sqrt(9 + 16 + 25)
  r = sqrt(50)
  r = 7.07

  ? = arctan (-4/3)
  ? = arctan (-1.33)
  ? = -53.13�

  f = arctan (sqrt(3^2+(-4)^2)/5)
  f = arctan (5/5)
  f = 45�

  So, the spherical coordinates of the point (3, -4, 5) are (7.07, -53.13�, 45�).

• Calculate the spherical coordinates of the point (-3, 4, 5):

  r = sqrt(-3^2 + 4^2 + 5^2)
  r = sqrt(9 + 16 + 25)
  r = sqrt(50)
  r = 7.07

  ? = arctan (4/-3)
  ? = arctan (-1.33)
  ? = -53.13�

  f = arctan (sqrt(-3^2+4^2)/5)
  f = arctan (5/5)
  f = 45�

  So, the spherical coordinates of the point (-3, 4, 5) are (7.07, -53.13�, 45�).

Summary

Spherical coordinates are a useful tool for representing points in 3D space. This system uses three angles and one length to precisely locate any point in space. The angles are the polar angle, ?, the azimuthal angle, f, and the radial angle, ?. The length is the distance, or radius, r. Spherical coordinates are used in a variety of applications, including navigation, physics, astronomy, and engineering.

FAQ

What are spherical coordinates?

Spherical coordinates are a system of coordinates used to specify positions or locations on a sphere. It measures the angle from the origin to a point on a sphere in three dimensions. It consists of three values - the radial distance, the polar angle, and the azimuthal angle.

How are spherical coordinates used?

Spherical coordinates are used in a variety of fields, including astronomy, navigation, and 3D computer graphics. They are also used to describe the location of points on the surface of a sphere, such as the Earth.