What is a Central Angle?

In geometry, a central angle is an angle whose vertex is at the center of a circle. A central angle is formed by two radii (plural of radius) of a circle. The central angle is equal to the measure of the intercepted arc. An intercepted arc is a portion of the circumference of a circle encased by two line segments meeting at the center of the circle

Forming a Central Angle

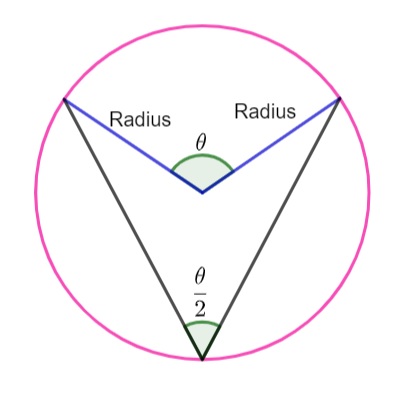
To better understand what a central angle is, let’s look at how one is formed. In the illustration below, there are two radii drawn to form a central angle θ°. The point where the two radii intersect is the vertex of the central angle. As you can see, the central angle θ° intercepts an arc on the circle’s circumference. This intercepted arc has a measure equal to that of the central angle θ°. It is twice the measure of the inscribed angle. An inscribed angle in a circle is formed by two chords that have a common end point on the circle.

Figure 1: Forming a Central Angle

Determining the Measure of a Central Angle

Now that we know how to form a central angle, let’s talk about how to measure one. There are two ways to find the measure of a central angle θ°. The first way uses degrees and requires you to know the formula for finding arc length. The second way uses radians and does not require you to use any formulas. We will go over both methods in this section.

Using the Arc Length formula (in degrees)

As we stated before, when you form a central angle θ°, it intercepts an arc on the circumference of a circle. This intercepted arc has a measure equal to that of your central angle θ°. If the intercepted arc length is known, then finding the measure of your central angle will be easy! To find the arc length, you need to use this formula:

Figure 2: Formula for Arc Length in Degrees

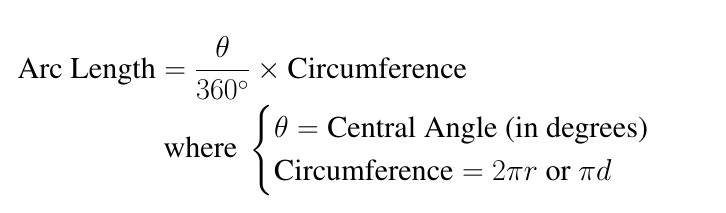
Example:

The circumference of a circle is 10π cm. The length of an intercepted arc is 25π/18. Find the central angle subtended by the arc.

Solution:

Using the formula from Figure 2, plug in the known values into our formula and solve for the central angle using algebraic manipulation:

Ok, now let’s try another example where we don’t know what our circle’s circumference is…

Using the Arc Length formula (in radians)

When we want to find the central angle ( in radians), the formula for finding the arc length is:

Figure 3: Formula for Arc Length in Radians

Example:

The radius of a circle is 9 inches. The length of an intercepted arc is 3π/2 inches. Find the central angle subtended by the arc in radians.

Solution:

Using the formula from Figure 3, plug in the known values into our formula and solve for the central angle using algebraic manipulation.

Notice how when working with larger numbers and decimals, it becomes increasingly important to take things slow and double-check your work along the way to prevent making careless mistakes that could change the entire outcome of your calculation!

Conclusion:

Central angles are angles whose vertices are at the center of circles. They are formed by two radii and intercept arcs on circumferences. To determine their measures, either use degrees or radians—but be careful when using larger numbers as decimal places can easily throw off your calculations! Thanks for reading and good luck in all your future geometric endeavors!

FAQ