What is Angle Bisector in Geometry?

Geometry is the branch of mathematics that deals with the properties of shapes and relationships between them. It's a fascinating subject that provides students with a wealth of knowledge and skills to help them understand the world around them and make sense of it. One of the important concepts in geometry is understanding angles and their properties. An angle bisector is an important concept in geometry that is used to divide angles into equal parts.

What is an Angle Bisector?

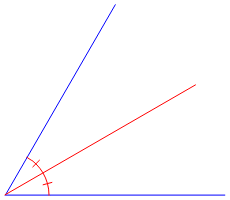
An angle bisector is a line segment that divides an angle into two equal parts. It's also known as the bisector of an angle. The line segment is perpendicular to the angle's two sides, and its length is always equal to half of the angle's total length. The angle bisector theorem states that the angle bisector divides the angle into two equal angles, each with a measure of half the original angle.

For example, consider an angle with a measure of 90 degrees. The angle bisector would divide this angle into two angles of 45 degrees each. Similarly, an angle with a measure of 60 degrees would be divided into two angles of 30 degrees each.

How to Bisect an Angle?

Bisecting an angle is the process of dividing it into two equal parts using an angle bisector. This can be done by drawing a straight line through the center of the angle, making sure that it is perpendicular to both sides of the angle. The line should be drawn so that it divides the angle into two equal parts.

To bisect an angle, first draw a line that is perpendicular to both sides of the angle. Then, draw another line that is parallel to one of the sides of the angle and intersects the first line. This will divide the angle into two equal parts.

The Angle Bisection Theorem

The angle bisection theorem states that the angle bisector divides the angle into two equal angles. This means that if an angle is bisected, the two resulting angles will be equal in measure. This theorem is especially useful when constructing shapes with specific angles, such as a triangle or a square.

To prove the angle bisection theorem, we can use the properties of similar triangles. If two angles of a triangle are equal, then the sides opposite those angles are also equal. This means that if two angles of a triangle are equal, then the triangle must be an isosceles triangle. Therefore, if an angle is bisected, the two resulting angles must be equal.

Practice Problems

To practice bisecting angles, we can use the following practice problems.

Problem 1

Bisect an angle with a measure of 30 degrees.

Solution: The angle can be bisected by drawing a line perpendicular to both sides of the angle. This will divide the angle into two angles of 15 degrees each.

Problem 2

Bisect an angle with a measure of 45 degrees.

Solution: The angle can be bisected by drawing a line perpendicular to both sides of the angle. This will divide the angle into two angles of 22.5 degrees each.

Problem 3

Bisect an angle with a measure of 60 degrees.

Solution: The angle can be bisected by drawing a line perpendicular to both sides of the angle. This will divide the angle into two angles of 30 degrees each.

Problem 4

Bisect an angle with a measure of 90 degrees.

Solution: The angle can be bisected by drawing a line perpendicular to both sides of the angle. This will divide the angle into two angles of 45 degrees each.

Problem 5

Bisect an angle with a measure of 120 degrees.

Solution: The angle can be bisected by drawing a line perpendicular to both sides of the angle. This will divide the angle into two angles of 60 degrees each.

Summary

In this lesson, we discussed angle bisector in geometry. We defined it as a line segment that divides an angle into two equal parts, and we discussed the angle bisection theorem. We also looked at how to bisect an angle, and we practiced bisecting angles with a few practice problems.

Angle bisector is an important concept in geometry, and understanding it will help students understand angles and their properties. With this knowledge, students will be able to construct shapes with specific angles, such as a triangle or a square.

FAQ

What is an angle bisector in geometry?

An angle bisector in geometry is a line segment or a ray that divides an angle into two equal parts.

Which is the best definition for angle bisector?

The best definition for angle bisector is a line segment or a ray that divides an angle into two equal parts.

How do you find the angle bisector in geometry?

To find the angle bisector in geometry, draw two lines that form the desired angle, then draw a line segment or a ray that divides the angle into two equal parts.

How does an angle bisector work?

An angle bisector works by dividing an angle into two equal parts. It is a line that bisects the angle and divides it into two equal parts.