The RHS Congruence Criterion for Proof in Geometry

In geometry, two figures are said to be "congruent" if they have the same size and shape. In other words, congruent figures can be superimposed on one another. Proving that two figures are congruent is often a key step in solving geometric problems. There are several different ways to prove that two figures are congruent.

In this blog post, we'll focus on one particular method known as the "RHS congruence criterion", which is written in full as Right-Hand Side congruence criterion.

The RHS criterion is used to determine if two right triangles are congruent. By this criterion, if the hypotenuse and one side of two right-angle triangles are the same, then the figures are congruent. Let's take a look at how this works with a few examples.

Example 1

Consider the following two figures:

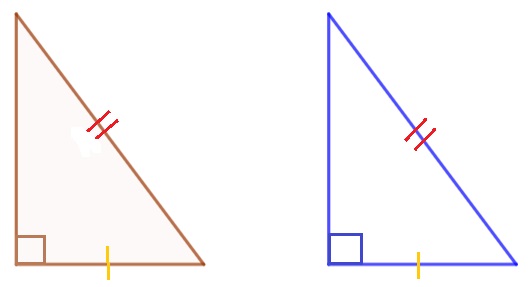
Since the hypotenuse and one side of the two right-angle triangles are equal in length, we can conclude that the figures are congruent.

Example 2

Now let's look at a different example:

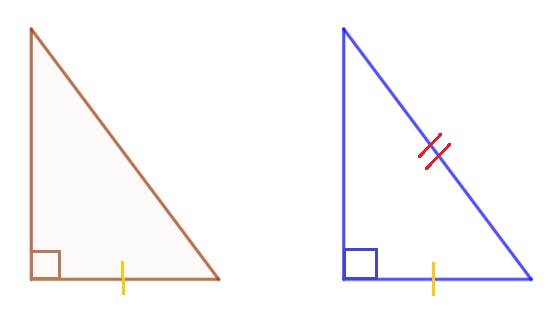
In this case, we can see that although one of the sides are congruent, the hypoteuse is not congruent. Therefore, we cannot conclude that the figures are congruent using the RHS congruence criterion.

Example 3

Finally, let's consider one more example:

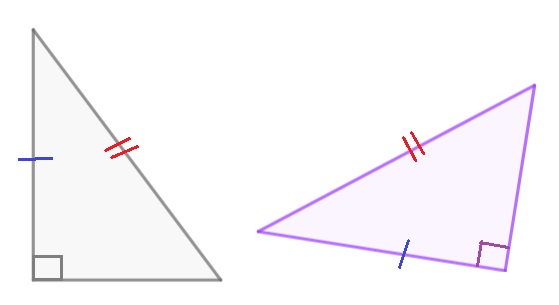
At first glance, it might seem like these two figures are not congruent. However, if we look closely, we can see that the hypotenuse and one of the sides has the same length. Therefore, we can use the RHS criterion to conclude that these figures are indeed congruent.

Conclusion:

As you can see, the RHS congruence criterion can be a useful tool for proving that two figures are congruent. However, it's important to be careful when using this criterion, as it's easy to make mistakes if you're not paying close attention to the details of each figure. Practice makes perfect! If you keep working at it, you'll be able to use this criterion with ease in no time.

FAQ

What does RHS mean in geometry?

RHS stands for "right-hand side." In geometry, the right-hand side of a figure is the side that contains the right angle.

What is the full form of RHS criterion?

The full form of RHS criterion is the "right-hand side criterion for proof in geometry." This criterion states that if the hypotenuse and one side of two right-angle triangles are the same, then the figures are congruent.

Explain the RHS criterion proof in geometry

The RHS criterion can be explained with the following example: Consider two figures, each with a right angle. If the hypotenuse and one side of the two right-angle triangles are the same, then the figures are congruent.

What is the RHS Condition for Congruence?

The RHS Condition for Congruence states that if the hypotenuse and one side of two right-angle triangles are the same, then the figures are congruent.

What is RHS congruence theorem of right triangles?

The RHS congruence theorem of right triangles states that if the hypotenuses and one other sides of two right triangles are equal, then the triangles are congruent.