How to Find the Area of an Ellipse
An ellipse is a closed curve that consists of two points, called foci, and the set of all points in a plane such that the sum of the distances from each focus to any point on the curve is constant. In other words, an ellipse looks like a flattened circle, as you can see in the image below.
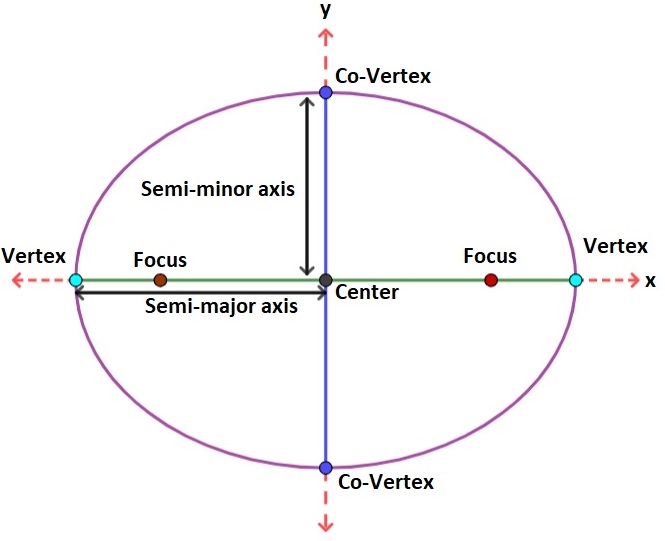
You might be wondering how to find the area of such a weird-looking shape. Luckily, there's a formula for that! In this blog post, we'll go over how to find the area of an ellipse. Let's get started!
The Semi-major Axis and Semi-minor Axis
The semimajor axis is the distance from the center to the vertex of our ellipse, while the semiminor axis is the distance from the center to the co-vertex of our ellipse. Having established these, the area of an ellipse is calculated using the formula:

Consider the ellipse with centre at (8,4) in the diagram below:
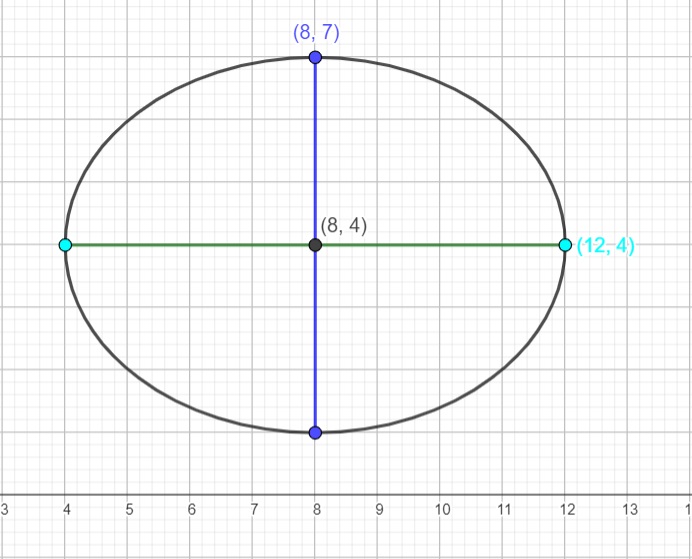
One of the vertices of the ellipse is at (12,4), therefore, the length of the semimajor axis:
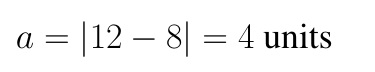
Next, one of the co-vertices of the ellipse is at (8,7), therefore, the length of the semi-minor axis:
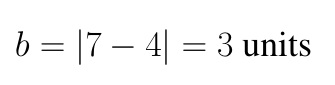
Substitute these values into the formula for the area:
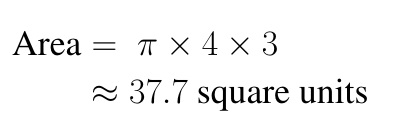
Example:
What if we are given the equation of the ellipse. How do we find the area?
Consider an ellipse with the equation 5x2+30x+64y2+128y=211, find the area of the ellipse.
When the equation of an ellipse is given, we can find the length of the semimajor and semiminor axes by first writing the equation in the standard form of an ellipse:
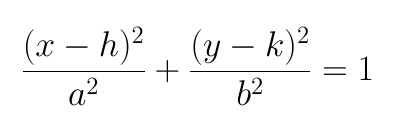
The equation is rewritten in the standard form below:

From the standard form:
- The length of the semimajor axis: a = 8
- The length of the semiminor axis: b = √5
Therefore, the area of the ellipse:
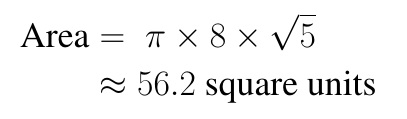
Conclusion:
As you can see, finding the area of an ellipse isn't nearly as complicated as it might seem at first glance! Whether you are given the graph or the equation, you can easily find the semimajor and semiminor axis which will then be used in the calculation. And that's all there is to it!