IntMath Newsletter: Putnam, review, Captive, cipher
By Murray Bourne, 12 Dec 2019
12 Dec 2019
In this Newsletter:
0. Season's greetings
1. New on IntMath: Putnam
2. The year in review
3. Math movies: Captive
4. Math puzzle: Cipher
5. Final thought: Imagine
0. Season's greetings
'Tis the season for special days. If you celebrate any of these, enjoy.
| Festival | 2019/20 date | Notes |
|---|---|---|
| Bodhi Day | 8 Dec, 2 Jan | "8th day of the 12th month" - so there's 2 of them |
| Pancha Ganapati | Hindu festival celebrated from 21 through 25 Dec | Based on the solstice |
| Solstice | 22 Dec | Celebrated in many cultures |
| Hannukah | 22 Dec to 20 Dec | Movable. Could be late November to early January. |
| Christmas | 25 Dec | "12 Days" finish on 6 Jan |
| Chinese New Year | 25 Jan (new moon) to 8 Feb (full moon) | Movable. Could start 21 Jan to 20 Feb |
1. New on IntMath: Solving a word problem (Putnam solution)
The William Lowell Putnam Mathematical Competition is held each year in early December. It's aimed at undergraduate students and has quite a reputation. Reader Pat Lachapelle participated in the competition this year and kindly provided a series of guest articles outlining the solution for an earlier competition question.
 |
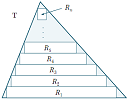See how to go about solving a word problem. Most of the concepts involved are around the grade 9 school level (age 15). There are 7 parts to the solution. |
2. The year in review
Thousands of readers have found the following useful or interesting during 2019. In case you missed any of them...
6 Most popular IntMath Newsletter resources, 2019
5 Most popular external resources, 2019
- Mathematical Symbols (by RapidTables)
- How to Study (MyDegreeGuide)
- Essence of Calculus (3Blue1Brown)
- MathGraph (online graphing tool)
- Breakthrough Junior Challenge (Explain a big scientific idea with a short video.)
6 Most popular blog posts, 2019
I wrote some of these years ago, but they are still popular - and/or causing controversy.
- How do you find the exact values for the sine of all angles?
- How to find the equation of a quadratic function from its graph
- Is 0 a natural number?
- How to reflect a graph through the x axis, y axis or origin
- How to draw y2 = x − 2
- Is cube root the same as raising to power 1/3?
6 Most popular forum questions, 2019
- Difference between disc method, washer method, and shell
- Is 270 degrees considered to be in the 3rd or 4th quadrant?
- How to find the first term and common ratio if the sum of first and third term is 20 and sum of fourth and sixth term is 540?
- Does Laplace exist for every function?
- How does plane analytical geometry apply in real life?
- Determining lambda for a poisson probability calculation
6 Most popular math lessons, 2019
- Domain and range (Functions and graphs)
- Convert polar to rectangular interactive (Complex Numbers_
- Derivative of sine, cosine and tangent (Differentiation)
- Solving DEs (Differential Equations)
- Singapore Toto (Counting and probability)
- Poisson Probabillity Distribution (Counting and Probability)
6 Most popular Tweets, 2019
- How to overcome fear of math tests
- "Your children need your presence more than your presents." [Jesse Jackson]
- The way math is written is (often) silly: Towards more meaningful math notation
- "Kindness is the language which the deaf can hear and the blind can see." [Mark Twain]
- "That man is richest whose pleasures are cheapest." [Henry David Thoreau]
- "Who you become is not about the traits you have. It's what you decide to do with them." [Adam Grant]
3. Math Movie - Device allows users to manipulate 3-D virtual objects more quickly
Here's an approach that could make quite a difference when students are learning about 3-D graphs.
 |
The device, called CAPTIVE, offers six degrees of freedom (6DoF) for users - with applications ranging from video gaming to medical diagnostics to design tools. See: Device allows users to manipulate 3-D virtual objects more quickly |
The article includes a video of the process in action. (It's a 2017 article, but nonetheless interesting.)
4. Math puzzles
The puzzle in the last IntMath Newsletter asked whether median or mean would be the best way to describe a typical value.
There were two parts to the puzzle, and correct answers with sufficient explanation were given by Dritan, Danish and Bob (who gets a special mention for pointing out it could be different depending on who the audience for the statistic is!).
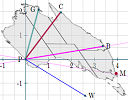
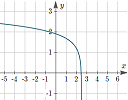
A good way to see what's happening in this puzzle is to draw graphs.
Person A "typically" could expect to earn around $90 (the median) per day. Clearly the mean (just over $75) is not "typical" of his earnings, so we would take the median to be the best statistic.
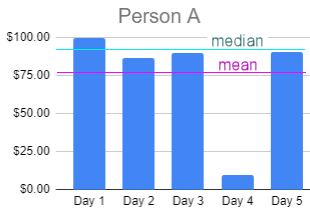
Person A's data
Person B, on the other hand, usually earns around $82 (the mean), not $72 (the median), so in this case, the mean would represent the "typical" earnings.
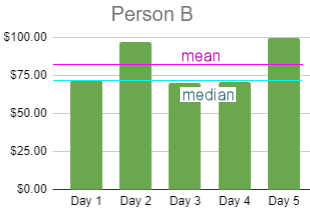
Person B's data
New math puzzle: Substitution cipher
A popular article at this time of the year is: The 12 Days of Christmas - How many Presents?
This cryptogram also involves 12. What is the value of each letter?
T W O
T H R E E
+ S E V E N
-----------
T W E L V E
You can leave your responses here.
5. Final thought - Imagine
Next year marks the 40th anniversary of John Lennon's murder.
My hope for 2020 is that more of us will get out of our echo chambers, start to listen to each other, and "live life in peace".
Imagine there's no countries
It isn't hard to do
Nothing to kill or die for
And no religion, tooImagine all the people
Living life in peaceJohn Lennon, Imagine
All the best to everyone for the holidays, and for 2020.
Until next time, enjoy whatever you learn.
See the 4 Comments below.
