Intmath Newsletter: Poly equations, charts, potential, water
By Murray Bourne, 31 Oct 2019
31 Oct 2019
In this Newsletter:
1. New on IntMath: Polynomial equations graph solver
2. Resources: Tilt Brush, charts
3. Math in the news: Lenses, integral equations
4. Math movies: Potential
5. Math puzzle: Square age
6. Final thought: Water
1. New on IntMath: Polynomial equations graph solver
After many reader requests, I rewrote a lot of the Solving Polynomial Equations chapter recently. I'm not a big fan of the way this topic is normally handled (via the Remainder and Factor Theorems) mostly because those techniques only work for low degree polynomials with "nice" numbers and involve an amount of guesswork. But I agree there is some benefit to learning the concepts.
The revised pages are:
Roots of a Polynomial Equation
I also added one new interative page:
 |
We can always use numerical approaches to finding the roots of equations (like Newton's Method). But I've always found (for the last 30 years while we've had such tools) that zooming in on the x-intercepts in a graph application is easier and quicker. We can get whatever accuracy we need by zooming in some more. |
2. Resources
(a) Tilt Brush: Painting from a new perspective
 |
Google's Tilt Brush for Vive, Oculus or Windows Mixed Reality lets you paint in 3D space with virtual reality. There's a lot of scope here for math students and teachers for drawing 3-D functions and vectors. |
Has anyone played with this? What's your experience been?
(b) Making charts easier to read at a glance
 |
Charts of complex data can be hard to comprehend. This new method from Columbia Engineering and Tufts University aims to develop easier to read data visualizations. See: New data science method makes charts easier to read at a glance |
3. Math in the news
(a) How One Mathematician Solved a 2,000-Year-Old Camera Lens Problem
 |
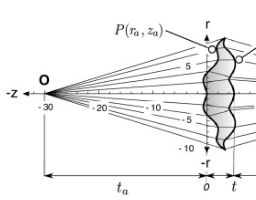Greek mathematician Diocles first reported on a problem most lenses have - spherical aberration. Here's a summary of a recent fix from Popular Mechanics: See: How One Mathematician Solved a 2,000-Year-Old Camera Lens Problem |
And here's the actual paper for those interested:
General formula for bi-aspheric singlet lens design free of spherical aberration (link no longer available)
(b) Metamaterials solve integral equations
 |
Solving integral equations has been a staple of science and engineering for hundreds of years. A new optical approach makes computer solutions significantly quicker. |
4. Math Movies - fulfilling our potential
(a) How we can help the "forgotten middle" reach their full potential
 |
Most of us fit in the "forgotten middle" - neither exceptional nor problematic. This talk gives some insights - for both students and teachers - on how such people can reach their full potential. See: How we can help the "forgotten middle" reach their full potential |
(b) The boost students need to overcome obstacles
 |
Everyone has a story - a reason why they have not met their own expectations or hopes for their lives. How we approach our obstacles can make a huge difference. |
5. Math puzzles
The puzzle in the last IntMath Newsletter asked about the probability involved in a given hexagon.
There were five attempts at an answer, and all were different. My approach was as follows.
Choose 1 for the length of each side of the octagon. That means the triangles and the square also all have side length 1.
The octagon's area is 2(1 + √2) (a well-known formula, or it can be derived from splitting it up into triangles).
The area of each (equilateral) triangle is √3/4 (half the base times the height) and we have 4 of them, so the total area of the triangles is √3.
The area of the square is 1.
The area of the blue parallelograms (kites) is the hexagon's area minus the area of the trangles and square.
Area blue = 2(1 + √2) − √3 − 1 = 1 + 2 √2 − √3.
So the probability is
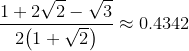
New math puzzle: Square age
If I said I was x years old in the year x2, it would mean for example, in the year 900 CE (AD), I was 30.
How old would somebody be if they could say that in the 21st century?
When is be the next century when nobody will be able to say the year is the square of their age?
You can leave your response here.
6. Final thought - water
Parts of Australia are undergoing the worst drought in recorded history. Some towns have already effectively passed "day zero" since trucking in water has become necessary. In many places, "day zero" will come sometime next year. Meanwhile, Capetown in South African recently averted a "day zero" situation.
For years scientists have been predicting such scenarios, and for years all we've seen is political football games.
Yes, the rains will come again. But it's more likely the next drought will be even longer. Many Australian farmers are talking about giving up, and this is in the country that promised to be the "food bowl of Asia".
You can't eat coal, and you can't drink oil.
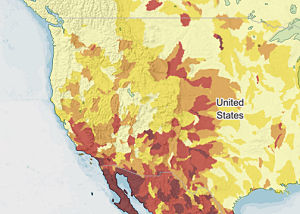
So how did Capetown do it? They imposed personal water restrictions of 50 liters per person per day and tough industrial restrictions ("Level 6B" water restrictions). By comparison, US citizens consume around 500 liters per day, New Zealanders consume 227 liters a day and in India, it's 120 liters per day.
See the state of your country in this Water Risk Atlas data map.
Until next time, enjoy whatever you learn.
See the 11 Comments below.
1 Nov 2019 at 12:31 am [Comment permalink]
It would be nice if you can publish about new techniques to teach math in the classroom
1 Nov 2019 at 4:37 am [Comment permalink]
@Raul: Thanks for the suggestion. Actually, just to let you know, every IntMath Newsletter contains some ideas that can be used in classrooms. For example, the roots of polynomial equations bit should not be taught algebraically any more, since it no longer makes sense. But for those cases where it's in the syllabus and must be taught, I provided some alternative ways to approach it.
1 Nov 2019 at 6:01 am [Comment permalink]
In the 21 century a 45 year olds age squared would work in the year 2025.
An age of 44 would work in year 1936 --too early, and a 46 year old would work in year 2116- too late.
In the 34 th century no one would have an age which when squared is the year. an age of 59 squared is less than 3500 and 60 squared is 3600. so no age squared is in the 3500's.
Answers were found using trial and error on a calculator with square and square root functions.
1 Nov 2019 at 6:12 am [Comment permalink]
Droughts are caused by weather. There was a bad on in the USA in the 1930's. It was commonly called the dust bowl. It destroyed many farmers. Most of the damaged lands are now productive farms again. Weather changes. It always has and always will. Man is far better off adapting to it as needed and always be aware that it will never stop changing. Call it political football if you want but political action is never going to control the weather. Politicians have no solutions; not because they are playing football, they just are not gods.
1 Nov 2019 at 4:34 pm [Comment permalink]
@Don: Weather causes droughts. This is obvious. What we are talking about is more severe droughts which are longer-lasting. Increases in greenhouse gases produces those. Politicians are in a position to do something about that one, but because of scientific ignorance, lobbying and disinformation by the powerful oil companies, and fear of losing elections, they continue to choose not to.
2 Nov 2019 at 2:19 pm [Comment permalink]
The answer is
The year 2025
2 Nov 2019 at 7:54 pm [Comment permalink]
I think I cheated by using Planmaker, but my answers are -
In 2025 a 45 year-old qualifies.
No-one will qualify in the 42nd century.
9 Nov 2019 at 8:15 am [Comment permalink]
1. Age 45, for the 21st century as it is the only integer whose
square falls between 2000 and 2099.
2. No age squared matches any part of the 36th century.
Age 59 x 59 = 3481
Age 60 x 60 = 3600
So no age squared falls during century 3500 to 3599.
( Solved by trial and error. Can equations be set-up to produce this result?)
9 Nov 2019 at 12:15 pm [Comment permalink]
Hi Murray, it is with regret but also with some satisfaction that I refer you back to the previous OCTAGON problem and the solutions offered.
Tomas Garza's solution 0.48236 is correct.
Taking octagon side = 1 makes sides of square and triangles = 0.95647
So there are no parallelograms!
(These differences can be seen on the original coloured diagram)
Proof:
Let x = side of square and also triangles.
Centre through square corner to perimeter = Centre through side of square to perimeter
0.5/cos(135/2) = sq rt 3 *x/2 + x/2
Solving for x yields 0.95647
Calculating for 4 such sided triangles yields an area of 1.58454
And for the square 0 91483
These added together gives the non blue area of 2.49937
This taken from the area of the octagon=
4.828427 - 2.49937 = 2.329057 for the blue area
So probability = 2.329057/ 4.828427 =
0.48236 = Answer
ps I'm thinking that you have planned these errors to check if we are paying attentions!
Cheers and thanks for all the good material that you present to us.
22 Nov 2019 at 4:38 pm [Comment permalink]
@Thomas: Thank you for alerting me to this! While I would love to claim I had "planned these errors to check if we are paying attention", but no, it was a mistake on my part.
After I read your comment, I actually had another go at constructing the octagon (using Geogebra), and it looked like this:
I started with a 1x1 square centered on the origin, constructed the equilateral triangles, and then the parallelograms, as per my earlier answer. Everything worked well, and I got the same probability I did before (0.422536).
However, the problem was I was seeing something that was not there - as Thomas pointed out, the parallelograms are wrong!
Constructing segments joining the apexes of the equilateral triangles makes this clear. (The light green/blue lengths are all the same, as I assumed, but my assumed angle for the bottom green/blue segment was wrong.)
As another check, I constructed a regular octagon on one of the sides of my irregular octagon, and once again, the problem with my solution is clear.
So I concede defeat... Tomas' answer is the correct one. ^_^
23 Nov 2019 at 2:58 am [Comment permalink]
Intelligence and honesty are the hallmarks of this great newsletter!
Thank you, Murray and Thomas, for your comments.
Cheers!