IntMath Newsletter: Quadratrix, resources, news
By Murray Bourne, 15 Jan 2020
15 Jan 2020
In this Newsletter:
1. New on IntMath: Quadratrix, quadratic
2. Resources: Desmos, e-book
3. Math in the news: Review and teaspoon
4. Math movies: Coin, key
5. Math puzzle: Race
6. Final thought: Real cost
1. New on IntMath
(a) Quadratrix of Dinostratus
Challenge: Using only a straight edge and compasses,
- Trisect an angle (divide it evenly into 3)
- Square a circle (construct a square with the same area as a given circle)
Don't work too hard on it, since neither is possible. The ancient Greek mathematicians put quite a bit of effort into solving these two problems.
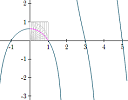 |
One of the approaches Hippias and Dinostratus used was to construct a quadratrix curve. |
The page has animations of how the curve is constructed, and some background.
(b) Solving quadratic equations - Po-shen Loh's method
I noticed a lot of my students would rather use the Quadratic Formula rather than solving a quadratic by factoring. One big reason for this is factoring can involve an amount of guesswork (finding 2 numbers that add to a certain number, and whose product is another number).
Mathematician Po-shen Loh recently outlined a method (not entirely original, and somewhat similar to completing the square method) which does away with the guesswork.
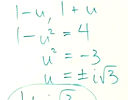 |
I added his method as alternative solutions in IntMath. See: Solutions for Examples 4 and 5, and Exercise 2 on the page: |
Po-Shen Loh is associate professor of mathematics at Carnegie Mellon University.
2. Resources
(a) Desmos Webinars
Desmos, the excellent free online graphing site, is offering some free Webinars over the next few weeks.
 |
These ones are mostly for teachers who want to create activities on Desmos. You can see details here: Desmos Webinars |
There are sessions on 14 Jan, 21 Jan and 28 Jan. Don't miss the links to recordings of previous seminars on the same page.
(b) e-book: A Programmer's Introduction to Mathematics
This is an interesting book, targeted at programmers, which aims to "show how to engage with mathematics".
 |
The book is by Jeremy Kun, engineer at Google. See: Pimbook |
You'll find:
- A (free) preview of the book
- A "pay what you want" PDF version of the whole book
- Demos of the concepts in the book
3. Math in the News
(a) The Year in Math and Computer Science
Mathematics is not a static thing. New discoveries and ways of thinking about old problems occur all the time.
 |
Here's a review by Quantamagazine of the main developments during 2019. |
The discussion about replacing "equality" with "equivalence" is interesting, and reminded me of my rant in The equal sign - more trouble than it’s worth?
(b) Storing YouTube in a teaspoon of DNA
We're heading for a "storage crisis". The amount of data generated each year (around 400 zettabytes by one estimate) will mean we won't have enough raw materials to manufacture all the optical and magnetic storage devices needed by the end of the century. We need to find other ways to store data.
One possible solution is to follow nature, and store the massive amounts of data in synthetic DNA. Scientists in Singapore are working on how to reduce the massive costs in such an approach.
 |
4. Math Movies
(a) The coin flip conundrum
Proability has a knack for throwing up counterintutitive situations.
 |
This TED-Ed video is an exploration of extensions to the simple coin flip. |
(This video is by Poh-shen Loh whose quadratic equation approach I mentioned above.)
(b) In the Key of Genius
I've been fascinated with savantism for a long time. Savants demonstrate extraordinary mathematical, artistic or musical abilities.
 |
Derek was born prematurely and is blind, had learning difficulties, autism but also amazing musical abilities, including perfect pitch and improvisation skills. |
So it begs the question - are we all born with such abillities and it just happens that some of us get to express them, while most of us don't?
5. Math puzzles
The puzzle in the last IntMath Newsletter involved a substitution cipher. No-one actually had a go at it (I know there are a lot of distractions in December...) so I'll leave it there and give you another chance to solve it.
New math puzzle: A race

Alana, Bob and Chaitali are running against each other in pairs over a 2 km distance. If Alana can beat Bob by 100 m, and Bob can beat Chaitali by 200 m, by what distance could Alana beat Chaitali (assuming their speeds are constant)?
You can leave your responses here.
6. Final thought - Paying the real cost

The "real" cost of any commodity should include the negative impacts the extraction and processing of that commodity have on all of us - the environment, our health, our future.
The IMF estimated that, in 2017, global fossil fuel subsidies grew to $5.2 trillion, or 6.5% of global GDP. [Source]
Why are we subsidising fossil fuel companies at all?
There are so many better things governments could be doing with our tax money...
Until next time, enjoy whatever you learn.
See the 10 Comments below.
17 Jan 2020 at 5:13 am [Comment permalink]
Are these puzzles meant to be solved by students?
17 Jan 2020 at 8:48 am [Comment permalink]
@Nathan: Anyone is welcome to have a go at the puzzles. There's often a good variety of approaches taken, sometimes due to experience.
17 Jan 2020 at 9:13 am [Comment permalink]
Alana beats Chaitali by 290m, because:
(At times solution can be found faster by assuming a value,
rather than taking time to derive an equation.)
So assume A takes 1000 secs to do 2000m.
Then B does 2000m - 100m =1900m
B’s speed = d/t = 1900/ 1000 = 1.9 m/s
Time for B to do 2000m = d/s = 2000/1.9 secs
C does 2000m - 200m = 1800m in the same time.
So C’s Speed = d/t = 1800/(2000/1.9) = 1.71 m/s
C’s distance covered in A’s time of 1000 s
= s.t = 1.71 x 1000 = 1710m
So Alane will be ahead of Chaitali by 2000 - 1710 = 290m = Answer
17 Jan 2020 at 10:31 pm [Comment permalink]
Let the runners be called A, B, and C.
Let A’s Speed be u m/s
Let B’s Speed be v m/s
Let C’s Speed be w m/s
The time for A to finish = the time for B to travel 1900.
Then 2000 ÷ u = 1900 ÷ v
v = (1900 ÷ 2000) u = 0·95 u
i.e. then B moves 0·95 of what A moves in one second.
The time for B to finish = the time for C to travel 1800.
Then 2000 ÷ v = 1800 ÷ w
w = (1800 ÷ 2000) v = 0·9 v
i.e. then C moves 0·9 of what B moves in one second.
B moves 0·95 of what A moved = 0·95 of 2000 = 1900 m
C moves 0·9 of what B moved = 0·9 of 1900 = 1710 m
Then A is ahead by 2000 - 1710 = 290 m
18 Jan 2020 at 3:14 am [Comment permalink]
Answer is 290 m.
Let alan, bob and chaitali speeds are a, b, c resp.
Alan beats bob by 100 m in 2 km race -> a/2=b/1.9
Bob beats chaitali by 200 m in 2km race. -> b/2=c/1.8
Solving these eqns for relationship between speeds of Alan and Chaitali gives
a/2=c/1.71
So, 2-1.71 km is 290 m. Alan beats Chaitali by 290 m.
20 Jan 2020 at 8:08 pm [Comment permalink]
In my opinion A will finish when C is 300m before final
25 Jan 2020 at 10:29 pm [Comment permalink]
Hi
Bob's speed is 1900/2000 = .95 Alana's speed
Caithali's speed is 1800/200 = .9 Bob's speed
Caithali's speed = .9 times.95 Alana's = .865 Alana's speed
Caithali's distance = .865 that of Alana = .865 times 2000 = 1710
Alana has beaten Caithali by 2000 - 1710 = 290m
7 Feb 2020 at 5:37 pm [Comment permalink]
Let us call the runners A, B & C.
We are told that when A finishes the course she is 100m ahead of B. When B finishes the course he is 200m ahead of C. So when A finishes the course how far is she ahead of C?
Speed(s)=distance(d)/time(t).
Let speed of A = s(A) etc.
So s(A)=2000/t(A).
At time t(A), B has run 1900m, so S(B) = 2000/t(B) = 1900/t(A)
Hence t(B)=20/19 t(A) = 1.053t(A)
At time t(B), d(C)=1800m, so s(C) = 2000/t(C ) = 1800/t(b)
Hence t(C)=20/18 t(b) = 1.111t(B) = 1.111 x 1.053t(A) = 1.1696t(A)
So s(C) = 2000/t(C) = 2000/(1.696t(A)) = 1710/t(A)
Therefore distance run by C at the time A finishes is 1710m. So A beats C by 290m
22 Feb 2020 at 2:18 pm [Comment permalink]
Hi Murray,
Regarding factoring a trinomial quadratic with rational coefficients, it can first be expressed the form cP(x) where c is a rational number in lowest terms and P(x) is a trinomial quadratic Ax^2+Bx+C with integer coefficients, where A>0, and where the coefficients have GCF=1. The signs of B and C give rise to 4 sign combinations: ++, -+, +-, and --.
If P(x) factors, then these lead to 4 sign combinations for the two "key numbers" to be found.
If C>0, then the two key numbers have the same sign, which is the same sign as B.
If C<0, then the two key numbers have opposite signs; the number with the greatest absolute value (i.e. the larger number) has the same sign as B.
To summarize the 4 cases:
++: key numbers have same sign, both positive
-+: key numbers have same sign, both negative
+-: key numbers have opposite signs, larger number positive
--: key numbers have opposite signs, larger number negative
Using the above, make a table for possible pairs of numbers with the desired product, checking as you go along whether or not they have the desired sum.
For example, for 8x^2+10x-3 is the +- case; the product must be (8)(-3) = -24, while the sum must be 10, so the key numbers must have opposite signs with the larger number positive. Pairs of possible key numbers having product -24 are listed in the table as follows:
(-1,24),(-2,12); the first pair listed has sum 23, so does not work, but the next pair has sum 10, and so the polynomial factors using the key numbers -2 AND 12, and no more table entries are required to exhaust all possible pairs with product -24, i.e. (-3,8) and (-4,6) are not needed.
As every integer has finitely many such possible pairs of factors, a table using these sign combinations will, for most high school problems, quickly yield the key numbers or show that P(x) does not factor (i.e. none of the pairs in the table has the required sum).
Best Regards,
Pete Halton,
Director: Math I Can Do Solutions Incorporated
23 Feb 2020 at 9:52 am [Comment permalink]
@Pete: Yes, that's what I'm doing on this page: Solving Quadratic Equations by Factoring.
The point is, a lot of students get fed up with the amount of guessing required, especially when their mental arithmetic skills are not up to scratch. It doesn't surprise me they'd rather go direct to the quadratic equation.