Quadratrix of Dinostratus

Page by Murray Bourne, IntMath.com. Last updated: 14 January 2020.

a. Background

Two problems captured the attention of the ancient Greek mathematicians. Using only compasses and a straight edge, they aimed to:

1. Trisect an angle (divide it evenly into 3)
2. Square a circle (construct a square with the same area as a given circle,)

The Quadratrix curve (from the Latin meaning "squarer") on this page was used by Hippias in 420 BCE in an attempt to solve the trisection problem, and by Dinostratus in around 350 BCE to square the circle.

A quadratrix is a curve whose y-values (ordinates) give us the area of another curve (in our case, the circle).

b. Quadratrix of Dinostratus construction

The Quadratrix of Dinostratus (also called "of Hippius") is an example of a kinetic curve, that is one created by moving parts. In this case, we start with a quadrant (a quarter circle) with radius `"OP"=1.` That radius rotates at a constant rate. Meanwhile, a point Q moves from the top left corner to the bottom left corner at a constant rate. A horizontal is projected from Q.

The curve that results from the intersection of those two segments is the Quadratrix of Dinostratus.

Assuming O is the origin and the horizontal axis is `y` and the vertical axis is `x`, the quadratrix curve can be described using parametric equations, as follows:

`x = (2tcot t)/pi`

`y=(2t)/pi`

for `0 <= t <= pi/2`

c. Animation

d. Reversing the axes

Next, we reverse the x- and y-axes (so they are in the "normal" orientation) to illustrate the curve we've created, this time using cartesian coordinates.

We plot 10 "typical" positions for the radius and 10 "typical" vertical segments in this next graph (vertical this time because of the axes reversal).

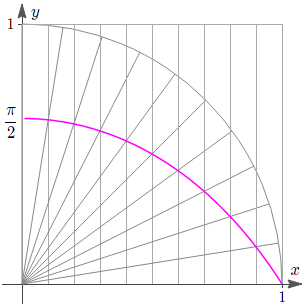
Quadratrix with axes reversed

The equation of the above curve is:

`y = xcot((pix)/(2))`

Here's the graph of that curve zoomed out and extended for more values of x.

You can zoom in or out using the slider to investigate this. The above image is included for context.

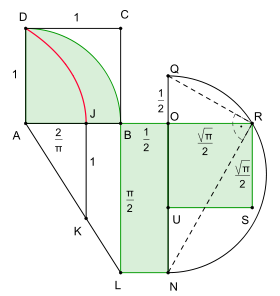
e. Squaring the circle using the quadratrix

Dinostratus' approach to the problem of squaring the circle was as follows.

The point of intersection with the horizontal axis of the curve DJ is `2/pi`. By projecting that point down by `1` unit (to K) and finding the intersection of the extension of AK with the extension of CB, we end up with a rectangle with the same area (`pi/4`) as the quadrant we started with. We can then form a square (via constructing the right triangle NQR) also having area `pi/4`. The (light green) quadrant, rectangle and square each have the same area.

We would just double the sides of that square to get the area of the circle with radius `1.`

Squaring the circle via quadratrix (Image source)

The trouble is, we can't construct the quadratrix using straight edge and compasses, and so we can't accurately position point J, meaning this is not an acceptable solution for squaring the circle.

You can see the full derivation of this result in Quadratrix of Hippias (Wikipedia).

f. Quadratrix of Tschirnhaus

Ehrenfried Walther von Tschirnhaus (1651-1708) was a German mathematician, physicist, physician, and philosopher, a contemporary of Isaac Newton and Gottfried Leibniz.

Tschirnhaus studied a curve he also called the "quadratrix", but the construction involved dropping a vertical line from the point P to the horizontal from Q, resulting in an inverse cosine curve.

Here is Tschirnhaus' curve, with the Dinostratus curve (dashed) for comparison.

g. Reversing the axes - Tschirnhaus

Once again we reverse the axes and see that we do indeed have a cosine curve, `y=cos((pix)/2).`

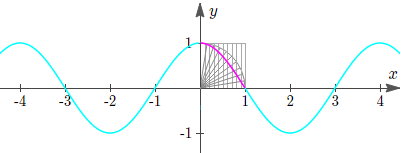
Quadratrix of Tschirnhaus with axes reversed