Witch of Agnesi

Page by Murray Bourne, IntMath.com. Last updated: 27 November 2019.

The Witch of Agnesi is a famous curve studied by Maria Agnesi, a rare 18th century female mathematician.

Below is an animation of the construction of this famous curve, as well as an animation of the slope of a tangent to an arctan curve, which is related to the "Witch".

a. Maria Agnesi

Maria Agnesi and her 1748 book, Instituzioni analitiche ad uso della gioventù italiana [Source]

Maria Agnesi (1718 - 1799) was the first known woman to write a mathematical handbook, Analytical institutions for use by Italian youth (originally Instituzioni analitiche ad uso della gioventù italiana), published in 1748. She was the first woman to be appointed as a mathematics professor at a time when it was unthinkable for most women to even get an education.

You can see more about her interesting experiences in Maria's Story.

b. Witch of Agnesi - not a witch at all

Maria included the "Witch of Agnesi" curve in her book, calling it averisera (meaning "versed sine curve", from the Latin vertere, "to turn".) It was discussed by other mathematicians before her, but her name is strongly associated with it now.

It turns out the term "witch" was associated with this curve when Cambridge Lucasian Professor of Mathematics John Colson translated Agnesi's handbook into English. He thought the name was avversiera (which means "adversary", "witch" or "a female evil spirit, a devil"). The mistranslation has stuck, but as we'll see below, the curve does bear some resemblance to a witch's hat.

c. Construction of the curve

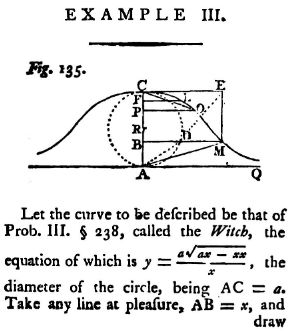
The following image (from Agnesi's original document, Instituzioni analitiche ad uso della gioventù italiana, page 485) shows how the "Witch" is constructed.

We start with a horizontal AQ, and regard A as the origin.

We construct a circle, sitting on AQ with diameter a = AC and center R(0, a/2).

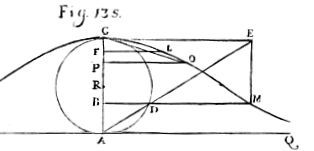
Original "Witch" of Agnesi from Instituzioni analitiche ad uso della gioventù italiana [Source, Fig 135, p. 485]

A segment is drawn from the origin A, to intersect the horizontal line CE at E. That segment intersects the circle at D. A horizontal is drawn through D to intersect an altitude EM dropped from the point E.

As the point D moves around the circle, the point M traces out a curve which is our Witch of Agnesi.

The general equation of the curve is:

`y = (a^3)/(x^2 + a^2)`

Here's an animation of this construction.

d. Witch of Agnesi animation

For the following animation, I chose the case `a=2`, giving us the horizontal at the top of the curve at y = 2 (shown in dashed grey). That segment also intersects the circle (shown by the grey dot), and a horizontal is drawn from that intersection point to intersect an altitude dropped from the line y = 2.

The resulting curve (the Witch, in dark green) is:

`y=8/(x^2+4)`

Things to do

This is quite a simple animation. You can "tidy up" what you see (making things clearer) by turning off some of the features, and you can pause the animation.

The above is an example of osculating curves. Any curve which touches another curve at one point having a common tangent is said to osculate (kiss) that curve.

e. Original document and equation

Here's Agnesi's original description of the construction of the curve (which says much the same as what I wrote above):

Original description of the construction of the curve by Agnesi from Instituzioni analitiche ad uso della gioventù italiana [Source, p. 392]

She sets `AB=x`, and at the end, she's discussing the similar triangles ABD and ACE, giving equivalent ratios `(AB)/(BD) = (AC)/(CE)`, and finally deriving the equation of the curve (in terms of the length `CE`) as `y = (asqrt(ax-x^2))/x`, where `x` is the distance `AB`.

The `y` and `x` in her description does not use the standard cartesian `y` (vertical) and `x` (horizontal) that I used in my description. Rather, it's the inverse. Click to see the proof that they are the same.

Proof of equivalence

Here's the relevant part of John Colson's 1801 translation, where he mis-names the curve "the Witch":

John Colson's English translation of the relevant portion [Source, p. 302]

Here's the curve with an elongated y-scale, giving more of an impression of a witch's hat:

f. Slope of the inverse tan curve animation

The astute among you will recognize the "Witch" curve as being related to the derivative of the curve `y = arctan x` (sometimes written `y = tan^-1 x`). See some background in Derivatives of the Inverse Trigonometric Functions.

We start with the function

`y = 4 arctan(x/2)` (in dark green).

The tangent to the function is shown in light grey.

The graph also includes the graph of the derivative of that arctan curve, the "witch" from above, in dashed grey:

`dy/dx = 8/(x^2+4)`

Run the animation, and you'll see how the "witch" describes the slope of the tangent of the `arctan` curve for different values of x.

The above graph does not have equal horizontal and vertical scale.