Maria’s Story

Maria lived in an age when most people − especially women − received no education at all. She was a brilliant girl but painfully shy.

After her mother died, Maria had to take over the house and look after all her 20 younger brothers and sisters.

Maria had a fascination with mathematics and gained a reputation as a competent mathematician. She managed to find time to write a famous book, Analytic Institutions, which brought together the brilliant calculus discoveries of Isaac Newton and Gottfried Leibniz.

Being a known sleepwalker, Maria would get up in the middle of the night and write down the solution for a math problem she’d been struggling with − while asleep! She would get up the next morning to find her answer waiting for her.

She was also a linguist and could speak French, Italian, Greek, Hebrew, Spanish, German and Latin by the time she was 11.

At just 9 years of age, Maria wrote and delivered an hour-long speech in Latin on women's right to be educated.

Always being concerned for those less fortunate than her, Maria would help the poor and needy in her area. She worked in a small hospital that she’d set up in her father’s house until she died at 81.

Who am I talking about? Maria Gaetana Agnesi (1718-1799), a resident of Milan. In 18th century Italy, women had very limited opportunity for education and found it hard to be taken seriously. Maria’s accomplishments are all the more remarkable because of the other duties she had to perform. Can you imagine trying to write a book with all those kids running around?

Maria Agnesi's Mathematics

Apart from her book, Maria was famous for a curve known as "The Witch of Agnesi". The witch part was just a translation error (it was supposed to be "turn"), but the name has stuck. She didn’t create the curve, but she studied it.

The Witch of Agnesi is formed as follows.

Take a circle and draw a horizontal line through the top of it.

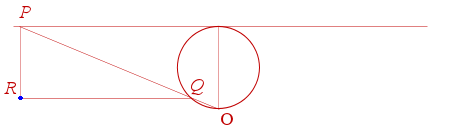
From a point O directly below the intersection of the line and the circle, draw a segment OP to intersect the horizontal line. Q is the point where OP intersects the circle. Draw a horizontal segment QR which intersects the vertical dropped from the point P. Put a (blue) dot at R.

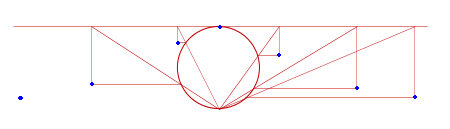
Move the point P along the horizontal line and join the bottom of the circle and drop verticals and horizontals as follows. Put blue dots on each intersection point.

If we draw enough of these and join the blue dots, we get the following curve, the Witch of Agnesi:

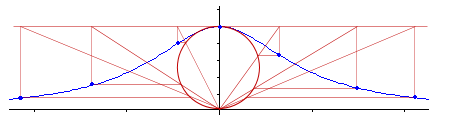
If the circle has radius a, then the equation of the Witch of Agnesi is given by:

The shape is quite similar to the bell-shaped normal curve that we come across in probability and statistics.

See the 11 Comments below.