IntMath Newsletter: Log graphs, challenges, news

29 May 2019

In this Newsletter:

1. New on IntMath: Logarithm function from its graph
2. Breakthrough Junior Challenge
3. Resources: Wolfram, MathGraph32
4. Math in the news: Computers and equations
5. Math movies: Calculus, Probability
6. Math puzzle: Bowling
7. Final thought: extinctions

1. New on IntMath: Finding the logarithm function from its graph

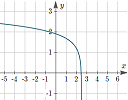This article explains how to observe the characteristics of a logarithmic graph to determine its equation. See: How to find the equation of a logarithm function from its graph?

2. Breakthrough Junior Challenge

One of the best ways to learn something is to explain it to someone else.

The Breakthrough Junior Challenge encourages students to create a short explanatory video. Prizes include a $250,000 post-secondary/college scholarship.

The overall idea, from the site:

Explain a big scientific idea in Physics, Life Sciences or Mathematics with a short video. You will have until June 15, 2019 at 11:59 PM PDT to submit your video (3:00 minutes max).

See these previous prize-winning videos made by students.

The number of submissions for math topics is quite low compared to the other categories. So, give it a go!

3. Resources

(a) Wolfram Language Webinars

Wolfram has released a new version of the Wolfram Language and Mathematica, and is offering 4 free Webinars to explain the new features.

I'm particularly looking forward to the June 12 one, which will cover:

Mathematics and Scientific Visualization
Calculus • Algebra • Complex Visualization • Geographic Visualization • Molecular Visualization

You can register here.

Of course, their main aim is commercial, but you can still learn a lot of worthwhile things by seeing how the experts make use of a powerful mathemtaical tool.

You may also be interested in Wolfram U, a series of videos which explores a range of math topics using Mathematica.

(b) MathGraph 32 - updated to javascript

I've featured MathGraph32 a few times before on IntMath. It's a cross-platform, cross-browser interactive graphing solution, with some very nice features. It's similar in many ways to GeoGebra, but I find it easier to use for many cases.

From the developer, Yves Biton:

"I have entirely rewritten MathGraph32 in JavaScript. It is still free under GNU GPL license. So no more use of Java, a new user interface without menu and new functionalities. Hope it will be useful because it was a tough job!"

MathGraph32 can be used:

1. Online (with easy to use menu icons); or
2. As a stand alone application (download page)

It also works on mobile devices.

Check out these tutorial videos in English, and here are some graph interactives.

4. Math in the news:

(a) Using computers to crack open centuries-old mathematical puzzles

Throughout history, a lot of mathematical research ended up in the "too hard" basket, because it was just impossible to do all the calculations necessary to draw a conclusion.

One such example is that of Diophantine Equations, the most famous of which was xⁿ + yⁿ = zⁿ, which has no whole number solutions when n is greater than 2, finally proved by Andrew Wiles after 300 years.

Diophantus of Alexandria was a 3rd century BCE Greek mathematician, often called the "father of algebra", as a result of his books on algebraic equations, called Arithmetica, a snippet of which is shown here.

The article Using computers to crack open centuries-old mathematical puzzles by Christopher Rasmussen, Associate Professor of Mathematics at Wesleyan University, explains in layman's language what the researchers aimed to do by using computers.

The actual paper talks about how they used Sagemath, an open-source computer algebra system, to solve cubic Ramanujan-Nagell equations, for example:

x³ + 3^k = qⁿ, where q is an odd prime.

One such solution is x = 2, k = 4, q = 89 and n = 1, giving:

2³ + 3⁴ = 89¹

(b) New memristor circuit solves linear equations in nanoseconds

An example of a simple linear equation written in matrix form is:

(See Matrices and Linear Equations for background.)

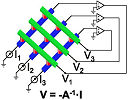A new circuit can solve large cases of such a system of linear equations in a single operation within a few tens of nanoseconds, much faster than using current or quantum methods.

It uses an analog method of in-memory computing, where one equation coefficient is stored as a unique resistance in one memristor (an electrical component that regulates the flow of current in a circuit and remembers the amount of charge that has previously flowed through it, retaining this memory even without power.)

The circuit was tested on a wide set of algebraic problems including:

1. Ranking of internet websites
2. Complex differential equations
3. Finding wave-function of an electron

See: Speeding up artificial intelligence

5. Math Movies

(a) Essence of Calculus - 3Blue1Brown

I've featured 3Blue1Brown's brilliant videos in earlier Newsletters. This time it's the series, Essence of Calculus.

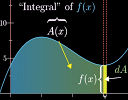If you are about to embark on studying calculus, this would be a great introduction: See: Essence of Calculus (playlist)

(b) False positive riddle

Mining unobtainium is hard work – the rare mineral appears in only 1% of rocks in the mine. But your friend Tricky Joe has something up his sleeve (involving conditional probability). See: Can you solve the false positive riddle?

6. Math puzzles

The puzzle in the last IntMath Newsletter asked about a general formula for a given sequence. There were an interesting range of responses.

Correct answers with sufficient reasons were submitted by Michael (who used modulus arithmetic) and Russell. Correct solutions (but with missing reasoning or details) were presented by: Gayathri, Christopher, Larry, Arun, and Nicola (who used a recursive approach).

New math puzzle: Bowling

In his latest bowling game, Raj scored 199 and this raised his average over a number of games from 177 to 178. What must he score in the next game to raise his average to 179?

You can leave your response here. Hint: If you present your answer with full explanation of how you obtained it, then others can follow your thinking and learn something from it.

7. Final thought - extinctions

Some years ago I was on a retreat in Malaysia. I enjoy going for walks in the early morning, and one day I followed a track into the (secondary) jungle. I was quite surprised to come across recent evidence (just hours old) of elephants using the same track. It could have been dangerous had I met those elephants, but I was excited to know wild elephants were still in the area. (Most of the virgin jungle in that area has been cleared for palm oil production, so it was doubly surprising.)

So I was saddened by the death this week of the last captive male Sumatran rhino in Malaysia, the last in a country that used to have plenty of them.

There is a real insanity of animal destruction going on in order to feed the irrational ivory, rhino horn, pangolin scale and shark fin markets.

Those who buy these products will need to consume fingernails when the animals are all gone. It will have the same effect on their libido and health.

Until next time, enjoy whatever you learn.

See the 11 Comments below.