IntMath Newsletter: First principles applet, resources
By Murray Bourne, 28 Nov 2017
28 Nov 2017
In this Newsletter:
1. New applet: Calculus first principles
2. Resource: ImmersiveMath
3. Math in the news: Proof School, GPU problem solvers
4. Math movie: Inspiration
5. Math puzzle: Intersecting parabolas
6. Final thought: Tenants
1. New applet: Calculus first principles
Sometimes the early concepts (usually called "first principles") of calculus can be a bit confusing.
 |
This new applet allows you to explore the concepts of differentiation and integration from first principles. |
2. Resource: ImmersiveMath
This is "the world's first linear algebra book with fully interactive figures".
 |
Immersive Linear Algebra contains some excellent animations and manipulatives that will help you to understand vectors, dot products, matrices, and determinants. |
The pages take a while to load, but it's worth it!
3. Math in the news:
(a) Proof School
A few years back I did some mathematics curriculum consultancy work for the newly-established School of Science and Technology, Singapore. Their approach is to incorporate various technologies into an interdisciplinary mix of art, design, media and environmental studies, on top of the national curriculum. I was reminded of that experience when I came across this article on Proof School, in California.
 |
Proof School is designed for "students who love math". Here is some background about the school, which has roots in the "math circle" concept, where kids can feel comfortable in a supportive and challenging math environment: |
(b) Innovative approach to solving massive problems on an ordinary PC
Russian scientists realized that if they used the GPU (graphics processor unit) of an ordinary PC, they could solve "260 million complex double integrals on a desktop computer within three seconds only". The best a supercomputer can achieve when solving the same problems is 2 to 3 days - and at a much greater expense.
 |
The GPU used a Nvidia GPU designed for use in game consoles. See: Russian scientists use a PC to solve complex problems tens of times faster than a supercomputers |
4. Math Movie: Exceptional teachers
(This is a bit late for last month's Teachers' Day, but still...)
Here's Stephen Hawking talking about his inspirational mathematics teacher:
"I have to admit – I wasn’t the best student – but with Dikran Tahta's support I became a professor of mathematics at Cambridge, in a position once held by Isaac Newton."
 |
See the short video: |
5. Math puzzles
The puzzle in the last IntMath Newsletter asked about different formulas for producing a given sequence of numbers.
Correct answers with explanation were provided by Phil, Karam and Chris.
New math puzzle: Intersecting parabolas
A quadratic graph with vertical axes has the general form:
y = ax2 + bx + c
Two parabolas with vertical axes can intersect in at most 2 points.
Now, consider the following graph. Here, I've rotated one of the parabolas:
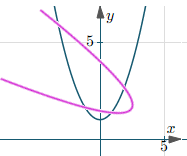
The equation of that rotated parabola has the form:
Ax2 + Bxy + Cy2 + Dx + Ey + F = 0
We can see the two parabolas intersect in 4 points, which is the maximum number of intersection points.
Or is it?
How is it possible for the coordinates of the five points (−1, 6), (3, −2), (1, 1), (0, 4) and (2, 0) to satisfy both of these quadratic equations?
2x2 − xy − y2 − 4x + 4y = 0
6x2 + xy − y2 − 16x + 2y + 8 = 0
You can leave your responses here.
6. Final thoughts: Tenants
Here's an apt quote from Rose Bird, Chief Justice of the California Supreme Court:
"We have probed the earth, excavated it, burned it, ripped things from it, buried things in it, chopped down its forests, leveled its hills, muddied its waters, and dirtied its air. That does not fit my definition of a good tenant. If we were here on a month-to-month basis, we would have been evicted long ago."
[Hat-tip to PiPo for alerting me to some of the items in this Newsletter.]
Until next time, enjoy whatever you learn.
See the 12 Comments below.
29 Nov 2017 at 4:22 pm [Comment permalink]
I smashed those equations and coordinates into Geogebra and it is true that all 5 points are contained within the two equations. I wasn't certain whether those equations really are parabolas so I had a bit of a Google:
The determinant of the matrix
is negative for both equations which means they actually represent hyperbolas. The determinant of the matrix
is equal to zero (Assuming the form of your equation is actually: 
) for both equations which means that both hyperbolas degenerate to their asymptotes and are therefore two intersecting lines.
29 Nov 2017 at 5:57 pm [Comment permalink]
Suggestion:
On future problems students might just be asked to submit a link to their work using Desmos, Symbolab, Wolfram, or Geogebra.
For example, on the two conic section equations, a link to Desmos shows they are the extreme cases where intersection of plane and cone yield line or crossing lines:
https://www.desmos.com/calculator/cy0l76inhm
How did we ever learn math with just a paper and pencil?
(-:
29 Nov 2017 at 6:45 pm [Comment permalink]
A look at the graphs of both equations reveals that they do not correspond to parabolas (I used the ContourPlot function of Mathematica for this purpose). In fact, if one looks for the solutions to the two equations jointly it turns out that one solution is x = 1, y = 1, but any pair (x, y) such y = 4 - 2x is also a solution (that includes, of course, the five points you mention). Using the discussion of the general equation of the second degree confirms this.
29 Nov 2017 at 8:24 pm [Comment permalink]
It must be just a coincidence.
30 Nov 2017 at 7:44 am [Comment permalink]
@Alan: Intriguing! What coincidence was that?
30 Nov 2017 at 11:52 am [Comment permalink]
It was with regard to the answer to item#5 (the puzzle), for which the link from "You can leave your responses here" led to ... here. But now I see that this is just the comment thread for the whole newsletter, so I should probably have been more specific.
The "coincidence" in my comment is just what led to the more than expected number of solutions.(But I was thinking that you probably didn't want me to give the solution away *too* directly.)
30 Nov 2017 at 5:02 pm [Comment permalink]
Hi Alan. I'm not sure if you experienced a glitch there.
The anchor text says "here" and the link takes you to the comment box on the post (which is where the user can respond). On the blog page itself, I'd prefer to put "below", but then that wouldn't make sense as the whole thing goes out in the actual Newsletter (where the "here" link of course also takes you to the Comments section of the page and "below" wouldn't make sense).
Got it re "coincidence"!
30 Nov 2017 at 6:04 pm [Comment permalink]
Thanks for your efforts in continuing with this newsletter.
A thought that struck me the other day.
Two spaceships leave planet Zog on a billion-year voyage to cross the universe. They are launched 100 miles apart and are told to maintain a parallel course always 100 miles apart so that one can always assist the other.The aim is to fly to point "A" one billion years from Zog and then return to Zog . One ship is green the other red. They are instructed respectively to leave behind green and red navigation buoys every 25 million years. 1 billion years out they turn round to come back.
As we all know space is expanding thus increasing the separation between galaxies etc and the navigation buoys closer to Zog have separated the most. How can the spaceships ever get back to their launch pads on Zog, assuming that it is still in range of the space-ships which have umpteen billion years fuel and food and water aboard?
In short, it is impossible to draw parallel straight lines in an expanding universe and all our parallel straight lines are an approximation.
Any thoughts..........?
2 Dec 2017 at 5:31 pm [Comment permalink]
@Bob: Intriguing question! Sounds like something Einstein would have loved to have tackled. What you said makes sense to me - a lot of our geometry only really "works" in our relatively limited Earth context.
4 Dec 2017 at 2:25 am [Comment permalink]
Good day Murray,
, why is one of the answers not there when changed to
Sorry, this is not a comment but a question.
Log equations:
In
2log (x×2)=2, thus log (x÷2)=2, giving only one answer?
Regards
Rika
4 Dec 2017 at 10:36 am [Comment permalink]
@Rika: There are some items in your question that don't seem to follow (like the product in the second expression and the divides sign in the third).
I rewrote it somewhat and answered it as a new Exercise (number 6) on this page: Logarithm and Exponential Equations
Hope it helps.
13 Dec 2017 at 3:58 am [Comment permalink]
In response to Bob Findlay I would add that you don't have to go all the way to Zog, or even have an expanding universe, for this problem to arise. It happens in any non-euclidean geometry - including that of the Earth's surface with "straight" lines interpreted as shortest paths on the surface (aka "geodesics" or "great circles").
If a railway line were built on Earth going all the way around the equator (with the tracks always exactly the same distance North and South) then they would not be "straight" in the sense of shortest distance, and if two "straight" tracks were laid starting from any two points then they would eventually cross (a quarter circle away from where they started)