IntMath Newsletter: Double springs, data, going viral
By Murray Bourne, 25 Oct 2017
25 Oct 2017
In this Newsletter:
0. Hiatus
1. Revised applet: Double Springs Interactive Graph
2. Resource: Wolfram Data Repository
3. Math in the news: Going Viral
4. Math movie: Maps
5. Math puzzle: Sequence formulas
6. Final thought: Learners
0. Hiatus
I've been swamped over the last few months with consultancy jobs, essential IntMath site maintenance and back pain, so I haven't had a chance to write an IntMath Newsletter in quite a while. Thank you for your patience - there's only 24 hours in a day!
1. New applet: Double springs
I recently revised the double springs applet, which is an example of a composite trgionometric curve. From a coding point of view, it's one of the most complicated applets in all of the ones on the site and was quite a challenge.
 |
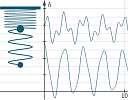You can find the applet about 1/3 way down this page: Composite Trigonometric Graphs Here's some mathematical background: |
2. Resource: Wolfram Data Repository
A promising future exists for those who can understand, interpret, manimpulate and visualize big data. The folks at Wolfram have made publicly available several datasets, which you can experiment with using your preferred code. (Python comes to mind, and Wolfram's own programming language is designed for easy data manipulation.)
 |
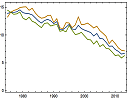Here is the background to the project from the Wolfram blog: Data Publishing that Really Works And here is the data repository: |
3. Math in the news:
(a) Catching the Great American Eclipse at 35,000 feet
In August there was a total eclipse of the sun passing over the entire USA. AlaskaAir took a group of eclipse watchers up to get a good view, and they had to make sure they maximized their customers' experience. The math behind the flight is quite interesting.
Threading the celestial needle: Catching the Great American Eclipse at 35,000 feet
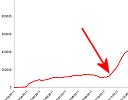
(b) Going Viral
These days, it gets harder to capture peoples' attention, and to "go viral" is the holy grail of most publishers. There are plenty of companies that will help you to get there (for a fee).
SearchLaboratory (a search optimization company) has an interesting mathematical take on how they applied a model developed for epidemic prediction in human health to the issue of "how much" and "how many" places you need to promote your content in order for it to go "viral".
 |
See: |
See especially the section, "Step 3: Applying the Stochastic General Epidemic Model".
4. Math Movie: Data maps
 |
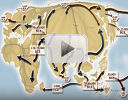I've been a lover of maps from way back, and so I enjoyed this TED talk where Danny Dorling talks about several different data visualization maps. See: |
5. Math puzzles
The puzzle in the last IntMath Newsletter asked about the angles of the hour, minute and second hands of a clock.
Correct answers with explanation were provided by Rick, Chris, Don, and Thomas. As usual, there were an interesting variety of approaches used, including "brute force VBA".
Update: A year ago (almost exactly) the Newsletter puzzle concerned a sheep in a circular field. Chris had another go at solving it by finding a few clever integrals, using "SciPy" (Scientific Python) software, which I mentioned earlier in this Newsletter.
New math puzzle: Sequence formulas
Example: The n-th term of the sequence 3, 5, 7, ... can be expressed using the formula an = 2n + 1, where n = 1, 2, 3, ... Now try these two.
(a) We have a sequence which alternates between 1 and −1 as follows:
1, −1, 1, −1, ...
Propose as many formulas as you can to represent the n-th term for this sequence.
(b) Bonus: Similarly, find formulas for the n-th term of the sequence:
3, −2, 3, −2, ...
You can leave your responses here.
6. Final thoughts: Learners
Here are two great quotes from moral philosopher Eric Hoffer (1898-1983):
"In a time of drastic change it is the learners who inherit the future. The learned usually find themselves equipped to live in a world that no longer exists."
"The hardest arithmetic to master is that which enables us to count our blessings."
Until next time, enjoy whatever you learn.
See the 4 Comments below.
