IntMath Newsletter: Angular velocity, face numbers, WIRIS
By Murray Bourne, 31 Oct 2016
31 Oct 2016
In this Newsletter:
0. Ad blockers
1. Linear & angular velocity applet
2. Your face in numbers: Microsoft's Face Detection app
3. Resource: WIRIS Calc
4. Math movie: Conspiracy theories & math
5. Math puzzles
6. Final thought
0. Ad blockers
Most of us cannot imagine how we'd cope without Google, YouTube, Facebook and Twitter. What keeps all of these coming into our lives for free? It's the same thing that's kept magazine, newspapers, television and other news services alive for many years: advertising.
Yes, you can easily block the ads on Google, YouTube, Facebook and Twitter, but please consider the outcome if everyone does that. All those services — and IntMath as well — would disappear.
1. Linear & angular velocity applet
 |
An object going around a circle has both an angular velocity (the amount of turn per time) and a linear velocity (the familiar distance per time). I recently added a linear and angular velocity applet where you can explore this concept, on the Applications of Radian Measure page: |
2. Your face in numbers: Microsoft's Face Detection app
Face detection is a fast growing research area because of its many applications in the security arena.
 |
Microsoft's Face Detection app is a lot of fun. You can upload any face picture and it will analyse the various parameters of the face (width between the eyes, nose and lips position, etc). It even takes a guess at the age of the person in the picture. For my picture, it was only a year or two out! (Ignore the "get started for free" button - that's for programmers.) |
On that page there's also "Face verification" to detect if 2 photos are of the same person, and also video face analysis near the bottom.
This could make a motivating class project on data gathering and intepretation.
3. Resource: WIRIS Calc
 |
WIRIS Calc (which I reported on earlier) is now in beta. This simple to use online computer algebra system has a lot of promise in an increasingly competitive field. It will solve problems in algebra, calculus and logic, and will also draw graphs. |
You can also save your worksheet to your local computer, to the Cloud, or as a PDF. Here's the documentation.
4. Math movie: Conspiracy theories & math
As I write, the debate about which US election conspiracy theory to believe continues to rage.
 |
From an early age, we look for patterns and usually the ones we find are actually there. But an interesting field of mathematics looks at how easy it is to find patterns just about anywhere, even where none were intended. This TED-Ed lesson explains how Ramsey Theory works. |
If you can vote in this, the worst election in living memory, please do.
5. Math puzzles
a. Bus route problem: The earlier problem (in the 29 Aug 2016 Newsletter) has been solved! Narendrakumar got the correct number of bus routes.
b. Domino puzzle: The puzzle in the last IntMath Newsletter asked about the sum of the fractions formed by the tiles in a domino set.
There was only one attempt to solve it, by Bill, and he was correct. (He gave 2 answers using different assumptions. but his first answer addresses the original conditions of the puzzle.)
The first row gives us (0 + 1)/1 = 1
The second row is (0 + 1 + 2)/2 = 3/2
The third row is (0 + 1 + 2 + 3)/3 = 2
And so on.
New math puzzle
 |
A sheep is placed in a circular fenced pen where it can chew grass all day. The farmer wants to make sure there is enough grass left in the pen for the following day, so she ties the sheep to one of the fence posts using a rope. How long does the rope have to be so the sheep can only eat half of the grass? |
You can leave your responses here.
6. Final thought: Responding
From the moment we're born, we start learning to respond to the things lfe throws at us. How much better off we'd all be if we saw each bad (and good) experience as a learning opportunity. It's all in our approach.
There's nothing in your life you can't learn from, if you respond with the right attitude. [Rick Warren]
Until next time, enjoy whatever you learn.
See the 20 Comments below.
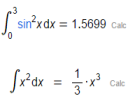
31 Oct 2016 at 8:52 pm [Comment permalink]
The rope should be equal to the circular fence diameter divided by two
1 Nov 2016 at 4:57 pm [Comment permalink]
It all depends on the size of the pen and whether the sheep is capable of eating half of the grass within it in the given time
1 Nov 2016 at 8:51 pm [Comment permalink]
Hi Murry
Love your information on maths
Do you know Rick Warren? I have read his book
Cheers
Laurie
3 Nov 2016 at 11:26 am [Comment permalink]
I look forward to the solution for the sheep problem. It did my head in.
Regards
Rhonda
4 Nov 2016 at 2:49 am [Comment permalink]
How many words we can get from the word " gammon " .. please I want to know the style of solution>>> thanks
4 Nov 2016 at 11:04 am [Comment permalink]
Hello Karam
This would be a good question for the IntMath Forum. Here's the appropriate section: https://www.intmath.com/forum/counting-probability-8/
4 Nov 2016 at 9:34 pm [Comment permalink]
Problem: construct a little circle inside a bigger circle so that the area of the little circle is 1/2 the area of the larger circle.
The area of the large circle is defined as: A=(pi)(R*R) where R is its radius.
The area of the smaller circle will be A(little)= (pi)(R(little)*R(little).
We want A(little)=1/2(pi)(R*R)
Substituting we find that R(little)=R/(square root of 2); which is approximately R/1.414.
So, from any point on the large circle, we would follow on a straight line to a point that equals R/1.414; take one of the fence posts from the enclosure and put it at that point, secure the goat with a corresponding length of rope.
Parenthetically, on the second day, the farmer can replace the fence post and let the goat run free inside the larger circular enclosure.
9 Nov 2016 at 4:25 am [Comment permalink]
We need to find the length of a rope L so that the shaded area is half the total area of the circle.
Half area of sheep pen
Draw a circle of unit radius (If radius is r it will cancel out anyway) and centre C.
Draw a diameter.
Call one end of the diameter Q.
Let QP be the required radius, where P is on the circle.
Let |QP| = L
With Q as centre and L as radius draw an arc inside the circle to cut the diameter at R.
Join Q to P and join P to C.
Angle PQC = Angle QPC = A, say.
Unit circle with arc from P with radius L to R on the diameter, showing angle A
Angle PCQ = π - 2A
Now, the Sine Rule for triangle ABC is:
where a is the length of the side opposite angle A, b is the length opposite B and c is the length opposite C.
By the sine rule it will be found that L = 2 cos A
The area of a sector of a circle with central angle θ and radius r is given by:
Using this, we find:
Sector PQC = 0·5(π-2A)
Sector PQC shaded
The area of a triangle with known sides a, b and included angle θ is given by:
Using this, we find:
Triangle PQC = 0·5 sin (2A)
The segment on PQ = sector PQC - ∆PQC = 0·5(π-2A) - 0·5 sin (2A)
Segment on PQ shaded
Once again using the area of a sector formula, but this time on QRP, we have:
Sector QRP = 0·5*L*L*A = 2A*cos (A)* cos (A)
Sector QRP shaded
Area enclosed between arc PQ, QR and arc PR
= 0·5(π-2A) - 0·5 sin (2A) + 2A*cos (A)* cos (A)
= 0·5(π-2A) - 0·5 sin (2A) + 2A*0·5*[cos (2A)+1]
= 0·25π
Area enclosed between arc PQ, QR and arc PR shaded
Let X = 2A and then get
0·5(π-X) - 0·5 sin (X) + X*0·5*[cos (X)+1] = 0·25π
Simplify and arrange and get
π - 2 sin X + 2X cos X = 0
Now I did a spreadsheet on solving this equation by Newton Raphson Method.
Let f(X) = π - 2 sin X + 2X cos X
f´(X) = 2X sin X
Initial guess was 3π/4
I came out with, after 3 or 4 runs with X = 1·90569372930988
A = 0·9528478647
The required length, L = 2 cos A = 1·158728473
Another way to solve the above equation is graphically. Here is the curve f(x) = π - 2 sin x + 2x cos x:
f(x) = π - 2 sin x + 2x cos x
Zooming in on the only feasible (realistic) solution for this problem, we see the curve cuts the x-axis near x = 1.9057, which is the same answer as we had before to 4 decimal places, and our length L will be the same at 1.16 m.
Zoomed in to find root
10 Nov 2016 at 9:38 pm [Comment permalink]
A different approach: Measure the heart girth of the goat. Although its' cross section will be ellipsoid, for a conservative approach assume that it is circular; find its' diameter and let that be represented by G. This would be the distance between two parallel constraints (such as slats) that would prevent the insertion of the object with this particular diameter. Let the height of the fence be represented by H...divide H by G to obtain the number of parallel constraints. The diameter of the fenced in area is represented by D...so, we will need to take the number of parallel constraints multiplied by D and add the product of( the number of parallel constraints ) and G to get the total length of the rope needed to pen in the goat. Tie one end of the rope to a fence post at a height of G above the ground, extend the rope to a directly opposite fence post post, continue the rope to a height of G above the first line or rope and return it to the directly opposite fence post, etc.
By the way, goats prefer more fibrous material than lush grass.
(I hope this makes sense).
14 Nov 2016 at 3:12 am [Comment permalink]
Length of rope
pen radius... depending on the length of the sheep's neck 😉
Explanation: let's just say I did some iterations in geogebra
14 Nov 2016 at 3:29 am [Comment permalink]
Well I Googled and I got it wrong 🙁
25 Nov 2016 at 8:58 pm [Comment permalink]
Dear Murray,
Glad to see there was no easy way.
Gerard
25 Nov 2016 at 10:12 pm [Comment permalink]
Well, there is no good answer. If the farmer has a very large pen, maybe half a million hectares as per some Australian stations, a standard unit Australian goat just cannot eat half the grass that grows in it in a day.
A correct answer should surely have some mathematical function showing dependency on size of pen and indeed density and quality of grass if need be, given standard unit Australian goat?
26 Nov 2016 at 9:51 am [Comment permalink]
@Bob: You're right! Perhaps we should have added at least a range of values for the radius of the pen, and a related value of the carrying capacity of the pen.
Real problems are always nicely messy! (Not that this is a "real" problem...)
3 Dec 2016 at 9:37 am [Comment permalink]
Tomas Garza sent me his solution done using Mathematica.
It was an interactive solution and the image shows the situation (r = 1.159) when the sheep can chew half the area of the blue circular pen.
Interesting solution, Tomas!
9 Dec 2016 at 8:28 am [Comment permalink]
Let R=radius of cir fence and l= radius of "circle" to be found.
Consider the chord C (extending between two intersection of the "circles" R and l. Let theta be angle formed from center of fence circle(between 2 radius and alpha, the angle centered on the fence circle by two segements of length l.
Now we have two area AR and Al. AR covers area between chord C and its arc on the circular fence. A second area Al covers the area between chord C and the boundary of grass eaten by the sheep. The sum of these two areas must be equal to
(1/2)R^2
AR = ((R^2)/2)(theta-sin(theta)
Al = ((l^2)/2)(alpha-sin(alpha)
Let R=1
(1/2)pi R^2 = AR + Al condition for 1/2 area
This gives
l= sqr(pi-(theta-sin(theta))/(alpha-sin(alpha)))
I was able to brute force values values of theta,and
alpha to find the l which satisfies the 1/2 area conditon.
I found l = 1.2 R
10 Sep 2017 at 6:49 pm [Comment permalink]
The grazing sheep problem has been in the back of my mind since you sent it out some time ago. I recently got a bee in my bonnet and decided to be done with it:
We can integrate the area under the two circles and solve for r such that area in both circles is half that in the pen.
We want to integrate under the area of the small circle until the two circles intersect, and then under the larger circle until it crosses the x-axis (at r).
To find the x coord for intercept of two circles -> set y equal
r^2 - x^2 = 1^2 - (x-1)^2
x = r^2/2
Integrate under the area of the small circle until r^2/2,
and then under the large circle until r
This area is now a quarter of the small circle area (integration only above x-axis)
That's the easy part. Now to solve… we give up and use Python:
It's still a bit tricky because the variable we want to solve for is in the limit. But it can be done with two functions for the integrands in terms of r. We can then integrate and solve for r with a reasonable starting guess of 1.
import numpy as np
from scipy.integrate import quad
from scipy.optimize import fsolve
def area1(x, r):
return np.sqrt(1**2 - (x-1)**2)
def area2(x, r):
return np.sqrt(r**2 - x**2)
def funky(r):
y1 = quad(area1, 0, (r**2)/2, args=(r,))
y2 = quad(area2, (r**2)/2, r, args=(r,))
return np.pi*(1**2)/4 - y1[0] - y2[0]
print("r =", fsolve(funky, 1)[0])
> r = 1.15872847302
I really enjoy the IntMath website and newsletters. Keep up the good work 🙂
21 Oct 2017 at 3:41 pm [Comment permalink]
@Chris: Good on you for having another go at this! Thanks also for including how you went about it - it's useful for others. Your solution looks good!
2 Nov 2017 at 8:48 am [Comment permalink]
Another answer for you, by my daughter-in-law, who has a 1st Class Honours Degree in Maths and Physics and thus is far better at such things than.
The length of the rope needs to be the diametre of the pen. Tie the rope across the diametre of the pen in such a way that the sheep neither wishes to jump over it nor crawl under it, thus assuming that there is enough grass in half the pen to keep it from being hungry.
A bit of lateral thought there.
2 Nov 2017 at 4:01 pm [Comment permalink]
@Bob: Great solution! I'm all for lateral thinking 🙂