IntMath Newsletter: Resources, hyperbolic discounting

By Murray Bourne, 08 Apr 2015

8 Apr 2015

In this Newsletter:

1. IntMath is 10 years old
2. Hyperbolic discounting
3. Resources
4. Math puzzles
5. Final thought - Teaching, by LKY

1. IntMath is 10 years old

When I started IntMath.com in April 2005 (it was in various forms before that), I was motivated by a desire to see more technological approaches in the teaching and learning of mathematics. Many students see math as calculation drudgery, however it can be - and should be - much more interesting and useful than that. At first, I used Flash and LiveMath to develop interactive math applets, but both of those technologies have gone the way of the dodo, and now I'm developing in javascriopt only.

Thank you to all my loyal readers through the years, and I hope everyone will enjoy the ride as much as I am!

2. Hyperbolic and exponential discounting

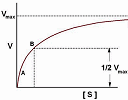There's some interesting mathematics behind hyperbolic discounting, a behavioral finance concept. Here's how it compares to exponential discounting.

Hyperbolic and exponential discounting

3. Resources

Here are some interesting things I've come across recently.

(a) Inverse Symbolic Calculator

This Inverse Symbolic Calculator is like a search engine for numbers with long decimal representations. It will give you a likely source for the number.

For example, I entered this decimal:

0.63661977236758134307553505349005744813783858296182

The calculator correctly identified this to be the expansion of 2/π.

This can be useful (for example) if you can calculate a value numerically, but need to know the function (or likely functions) that are behind the number.

(b) GraphFree

Here's a versatile online grapher: GraphFree. You can produce implicit, polar, parametric, piecewise, slope field and x-y scatter, as well as ordinary explicit function graphs. Output is given as an image, which you can copy and paste to your own document.

Use the online keyboard (real keyboard entry other than numbers may give error messages).

(c) WIRIS Calculator

WIRIS is an online calculator with graph capability. It also handles calculations in polynomials, statistics, linear algebra and calculus.

You can save your calculations (and graphs) to Google Docs for later use. Go here for documentation.

(d) Story of Mathematics

The Story of Mathematics gives consise summaries of the major players in the history of mathematical development. There are plenty of explanatory diagrams making this a useful resource for getting an overview of the contributions by important mathematicians.

(e) Girls really should do math and science

This article summarises a recent study showing the benefits to girls if they have some science, technology, engineering or mathematics (STEM) in their education:

Girls are better off choosing science at school

4. Math puzzles

The puzzle in the last IntMath Newsletter asked about a diagram that suggested the value of pi was 4.

The correct explanation for why it was wrong was given by Rajan, Thomas, and Tomas. (Tomas was the only one who addressed my other question, about why the continuous curve for the integer problem was not the most appropriate.)

Here's another way of looking at that pi problem. If we do a similar process, but on the inner square, we find it has width around 0.707 and so giving a first estimate for pi as 2.828. But if we push the middle half of each side out as shown, we get a perimeter which suggests pi is greater than 3.14!

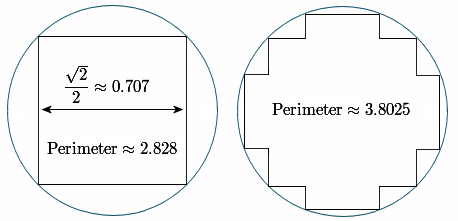
pi inner polygon

Of course, the limits from each side should approach the same value. Hence the thinking is flawed.

Here's how it should be done. Our initial square should have been broken up so the sides are tangent to the circle, using regular polygons with increasing numbers of sides. In the following diagram, I've constructed an octagon around the outside of the circle, and this gives an approximation for pi of 3.3137. In the one on the right, I've found the perimeter of the inner octagon to be 3.0615.

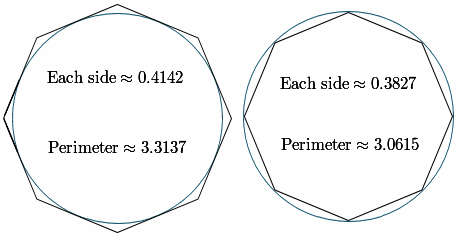
pi inner and outer tangential polygons

If we create polygons with increasing numbers of sides, the outer and inner perimeters will tend to the known value of pi.

This is similar to the approach taken by Archimedes around 250 BCE. (He was actually looking for the area of the circle.) There's a neat interactive on this page showing what Archimedes did: Approximating Pi.

And finally, here's Vi Hart's explanation of the Pi = 4 circle problem:

Rhapsody on the Proof of Pi = 4

New math puzzle

We have three points P, Q and R on the co-ordinate plane at (0, 8), (6, 0) and (x, 12) respectively. If 0 < x < 6 and area ΔPQR = 20 unit², what is the value of x?

Leave your responses here.

4. Final thought - Lee Kuan Yew quote

I've lived in Singapore now for nearly 20 years. It's a great place to be a teacher, since education is taken seriously and given the resources needed to produce (generally) good results. The current prime minister is a mathematics major (a rarity among world leaders).

The "founding father" of Singapore, Lee Kuan Yew, passed away last week. While his policies were often criticized in the West, he was responsible for producing a successful small country, where racial and religious harmony is a top priority, where there is full employment, high national savings and little debt, and which for the most part is safe, clean and green.

Here is LKY's thoughts on teaching.

Lee Kuan Yew quote

RIP, LKY.

Until next time, enjoy whatever you learn.

See the 16 Comments below.

Posted in Intmath Newsletters category - 08 Apr 2015 [Permalink]

Tags: Graphs, Interactive, Technology

16 Comments on “IntMath Newsletter: Resources, hyperbolic discounting”

Brian says:
8 Apr 2015 at 11:23 pm [Comment permalink]
Thank you for ten years on the Internet with your free, innovative math website.
Don Cohen says:
8 Apr 2015 at 11:32 pm [Comment permalink]
Murray, can you change the infinite repeating bimal ,010010010... to a non-binary fraction? Does that make sense?
Murray says:
9 Apr 2015 at 12:05 am [Comment permalink]
Hi Don

I'd probably proceed as follows (to get it into base 10, at least):

Let x = 0. 010 010 010 010...

= 010₂/2³ + 010₂/2⁶ + 010₂/2⁹ + 010₂/2¹² + ... [1]

Multiply both sides by 2³ = 8:

8x = 010₂ + 010₂/2³ + 010₂/2⁶ + 010₂/2⁹ + ...[2]

Subtract [1] from [2]:

7x = 010₂ = 2

So x = 2/7
Christian Mills says:
9 Apr 2015 at 12:15 am [Comment permalink]
I have an interesting solution to this problem that allows us to avoid using trigonometry. First, we must draw a triangle with vertices at the 3 points given and a rectangle around the triangle. This rectangle will have vertices at (0,0), (6,0), (6,12), and (0,12). The area of this rectangle is 72. If we subtract the area of the 3 right triangles formed inside the rectangle and outside the triangle from 72, we get the area of the triangle, 20. So, here is the resulting equation:
72-[.5(8*6)+.5(4*x)+.5(6-x)(12)]=20.
This reduces to 4x=8, where x=2.
Michael El-Jiz says:
9 Apr 2015 at 2:34 am [Comment permalink]
Hi Murray,
Any chance you could incorprorate LaTeX in the comments sections? Would be super cool!
The area of a triangle is the distance between a vertex to a segment times the length of that segment divided by two.
Area = PQ*RM/2 where M is the orthogonal projection of R on (PQ)
We know the length of [PQ]
[PQ] = sqrt(6^2 + 8^2) = sqrt(36 + 64) = 10
The equation for (PQ) is 0 = 4x/3 - y + 8
so RM = |4x/3 - y + 8| / sqrt( (4/3) ^ 2 + 1) = (4x-12)/5
Area = PQ*RM/2= (4x-12)*10/5 = 8x-24 = 20
x = 5.5, which fits the constraints!
Guido says:
9 Apr 2015 at 4:59 am [Comment permalink]
PQ = (8^2 + 6^2)^0.5 = 10
area PQR = 20 = 10*h/2
h = 4
angle (PQo) = arcsin(0.8) = 53.13°
equation PQ : Y = tg(-53.13°)*x +8 = -1.33*x +8
intersectionpoint(Z) : y= 12 = -1.33x + 8
x = -3 -----> Z(-3;12)
angle (ZQ and Y=12) = angle (PQo) = 53.13°
ZR = 4/sin53.13° = 5
oR = X = 5 -3 = 2
Therefore R(2;12)
Darrell says:
10 Apr 2015 at 7:33 am [Comment permalink]
Let vectors to (0,8), (6,0), and (x,12) be P, Q, and R, respectively. The area of the PQR triangle is half the parallelogram formed by vectors P - R and Q - R, i.e. these vectors form adjacent sides of the parallelogram.

The equation for solving the problem is: 1/2 | (P - R) x (Q - R) | = 20 sq units,
i.e. 1/2 the absolute value of the cross product of vectors P - R and Q - R = 20 ... Doing the vector algebra produces an answer of x = 2 ...

So vector R = (2, 12) ...
yousif taha says:
10 Apr 2015 at 12:57 pm [Comment permalink]
area of triangle = 1/2 * b * h
20 = 1/2 * 10 * h
therefore h = 4
perpenducular distance between point and line

h = (4x+3y-8)/sqr(16+9)
4 = (4x+3*12-8)/5
20 = 4x + 28
x = 2
Charles Kibasa says:
11 Apr 2015 at 3:24 am [Comment permalink]
the triangle lies in the rectangle with area 72. the value x is obtained by subtracting the areas of the other triangles inside the rectangle where the equation 72-2x-6(6-x)-24=20 applies. and x=2.

Joseph says:
12 Apr 2015 at 4:54 pm [Comment permalink]

Using the determinant method, we can find the value of x.
Given P(0,8), Q(6,0), R(x,12) and Area = 20,

           [1  1  1 ]        [1 1 1 ]
Area = 1/2 [x1 x2 x3]  = 1/2 [0 6 x ]
           [y1 y2 y3]        [8 0 12]
     = 1/2[6 x ] - 1/2[0 x ]+ 1/2[0 6]
          [0 12]      [8 12]     [8 o]
     = 1/2[(72-0)-(0-8x)+(0-48)]
     = 1/2[72-(-8x)+(-48)] = 1/2(72+8x-48)
     => 1/2(24+8x)= 20;=> 24+8x = 40; 8x = 16;=> x = 16/8
     => x = 2.

Thomas A Buckley says:
15 Apr 2015 at 8:26 am [Comment permalink]
Answer x=2
One of several methods to solve this:
If one vertex is put at (0,0), then
Area of triangle A = | PxRy - RxPy | /2 . . .Eq1

Shifting the triangle left 6 units will put Q(6,0) at (0,0)
Then A=20, Px=-6, Ry=12, Rx=?, Py=8
Placing these values in Eq1, yields Rx=-4
Shift triangle right 6 units puts Rx = 2 = Answer
Tomas Garza says:
17 Apr 2015 at 9:31 am [Comment permalink]
Use the formula to obtain the area of a triangle using the 3 x 3 determinant D, whose rows are (0, 8, 1), (6, 0, 1) and (x, 12, 1):
area = 0.5 |D|, and solve the equation 0.5 |D| = 24 for x.
The solution is x = 3.
Grant says:
24 Apr 2015 at 10:04 am [Comment permalink]
To find x we will find the parallelogram that contains 2 × ΔPQR.

First we'll find the base of this parallelogram or PQ.

${P}{Q}=\sqrt{{{{\left({0}-{6}\right)}}^{2}+{{\left({8}-{0}\right)}}^{2}}}$

We know this parallelogram has area 2 × ΔPQR = 40 units².

The area of a parallelogram = bh.

So

40 = 10h or h = 4.

We now know there is a parallel line 4 units away from PQ that forms the other side of the parallelogram.

The gradient of PQ is:

${m}={\frac{{{0}-{8}}}{{{6}-{0}}}}=-{\frac{{4}}{{3}}}$

We can find a point on this new line being 4 units away from Q.

New point =

${\left({6}+{4}{\cos{{\left({\arctan{{\frac{{3}}{{4}}}}}\right)}}},{4}{\sin{{\left({\arctan{{\frac{{3}}{{4}}}}}\right)}}}\right)}={\left({9.2},{2.4}\right)}$

because arctan(3/4) is the angle between the x-axis and the perpendicular line, of length 4, from PQ.

We can now find the equation of this new line as:

${y}-{2.4}=-{\frac{{4}}{{3}}}{\left({x}-{9.2}\right)}$

or

y = (−4x + 44)/3

Because PR makes the sides of the parallelogram, this new line also passes through R.

Substitute R(x,12) in the new line equation:

12 = (−4x + 44)/3

36 = −4x + 44

4x = 8

x = 2
Amin and Nicole says:
24 Apr 2015 at 10:41 am [Comment permalink]

Area ΔPQR = 20 unit²

A₁ + A₂ + A₃ + Area ΔPQR = A_rectangle

A₁ = (1/2)(4)(x) = 2x

A₂ = (1/2)(8)(6) = 24

A₃ = (1/2)(12)(6 − x) = 36 − 6x

A_rec = 12 × 6 = 72

So

2x + 24 + 36 − 6x + 20 = 72

4x = 8

x = 2
Charles Kibasa says:
24 Apr 2015 at 1:44 pm [Comment permalink]
It is very interesting to see so many ways that were used by the participants to reach at the solution.
George Varelas says:
30 Apr 2015 at 1:34 am [Comment permalink]
A1 + A2 + 20 = [(2 + 6)/2]*12 = 48 (trapeze),
A1 + A2 = 28
[(12 - 8)/2]*x + 6*8/2 = 28
2x + 24 = 28
2x = 2
x=2

IntMath Newsletter: Resources, hyperbolic discounting

1. IntMath is 10 years old

2. Hyperbolic and exponential discounting