IntMath Newsletter: Fourier graph, resources
By Murray Bourne, 29 Aug 2016
29 Aug 2016
In this Newsletter:
0. Top 100 Math Blog
1. Fourier Series interactive graph
2. Why such interest in exact trigonometric ratios?
3. Free online course: Computing and calculus for applied statistics
4. Math movie: Five Principles of Extraordinary Math Teaching
5. Math puzzles
6. Final thought: Perpendicular
0. SquareCirclez blog gains place in Top 100 Math Blog list
 |
I was humbled this week to receive notice that SquareCirclez (the IntMath Blog) has been included in a list of the "Top 100 Math Blogs". See the full collection here: |
1. Fourier Series interactive graph
 |
I recently updated the Fourier Series interactive graph so it works better on mobile devices. You can explore the concept of adding periodic terms to obtain square and saw tooth waves (and an odd "cos blip" wave). Fourier Series is used in electronics and electrical engineering. |
2. Why so much interest in exact trigonometric ratios?
 |
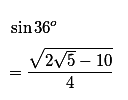One of the most popular IntMath blog posts is How do you find exact values for the sine of all angles? which I published back in June 2011. I'm surprised that it's generated so much interest over the years (with over 60 comments). Can anyone tell me why? |
I mean such calculations are an interesting diversion from a mathematical point of view, but the results are not particularly useful for most people (since most of us use decimal approximations of trigonometric ratios).
Are students given assignments where they need to find all those exact ratios? Is it just one of those mysteries that people sometimes get into? Any ideas, please respond here.
3. Free online course: Computing and calculus for applied statistics
The course "Computing and Calculus for Applied Statistics" is starting this week. This course is intended to give students a useful background in math and computing, for using and studying applied statistics. The material is directed only to applications in statistics. It is (mostly) a self-study course, but with on-line guidance and interactivity with other students through the piazza resource.
The course is completely open. To register, send an email to [email protected].
Student assignments are of several types:
- Multiple-choice drills on the tutor-web;
- Student-submissions and peer-review of new multiple-choice drills (tutor-web);
- Student-submitted worked examples (submissions in LaTex).
The final grade will be based on the tutor-web grade as well as participation in the course (via piazza).
4. Math movie: Five Principles of Extraordinary Math Teaching
 |
In this TEDx talk, Dan Finkel (creator of the award winning mathematical board game Prime Climb) gives suggestions on how to make math less intimidating. I liked what he had to say about ownership of learning. |
The board game reminded me of the Tesla Map to Multiplication.
5. Math puzzles
The puzzle in the last IntMath Newsletter asked what day of the week was the first day of the 20th century.
Correct answers with sufficient explanation (which included reasoning) were given by: Γιώργος and Ben.
Of course, the question didn't say that you were supposed to do it without the aid of calendars or a search, but it doesn't take a lot of mathematical thinking to just Google it!
One of the first issues with this question is to decide what is the first day of the 20th century. Was it 1st Jan 1900, or 1st Jan 1901? (Don's and Mawaza's answers would have been correct if it was the former, but actually, it's the latter. Ben covered his bases by including both.)
New math puzzle
A city's bus routes have the following characteristics:
- There are exactly 11 bus stops on each route
- It is possible to travel between any 2 bus stops without changing routes
- Any 2 bus routes have exactly one bus stop in common
How many bus routes are in this city?
You can leave your responses here.
6. Final thought: Perpendicular
Frances Willard, American educator and women's suffragist used some mathematical concepts when she optimistically said:
"This seems to be the law of progress in everything we do; it moves along a spiral rather than a perpendicular; we seem to be actually going out of the way, and yet it turns out that we were really moving upward all the time."
Which brings me to this delightful image:
Until next time, enjoy whatever you learn.
See the 6 Comments below.
29 Aug 2016 at 3:07 pm [Comment permalink]
1 route
This solution allows moving from any of the 11 stops to any of the remaining 10.
The second condition "any two" does not apply since only one route. More than 1 route, say 2, with one common stop would demand changing route to satisfy the "any two", but changing routes is not allowed. Thus 1 route.
30 Aug 2016 at 3:08 pm [Comment permalink]
Answer of puzzle Aug 29 2016
12 bus routes (and 66 bus stops)
I will send you this answer with
detail.
31 Aug 2016 at 4:20 pm [Comment permalink]
Hello, Trigonometric ratio: to me intellectually interesting but I don't have any particular use for them. A not so helpful answer is " like Everest, because it's there "!
Kind regards, Roger
20 Sep 2016 at 2:12 am [Comment permalink]
nomber of routs is 12
20 Sep 2016 at 1:22 pm [Comment permalink]
Let the number of bus stops on a route be n then the number of possible routes is n^2-n+1. That is for 11 stops the possible routes are 121-11+1=111 !!! (With given condition.) There will be one and only one route to connect any two bus stops.
22 Sep 2016 at 11:01 am [Comment permalink]
Exact trigonometric ratios are inherently interesting in themselves !