IntMath Newsletter: Fourier interactive, 2012 summary
By Murray Bourne, 18 Dec 2012
18 Dec 2012
In this Newsletter:
1. New interactive: Fourier Series
2. Christmas
3. Most popular articles of 2012
4. Looking ahead - 2013
5. Math puzzles
6. Friday math movie: The Mathematics of History
7. Final thought - treating others
This is the last IntMath Newsletter for 2012. It's a bumper issue with lots of (hopefully) interesting reading.
1. New interactive: Fourier Series
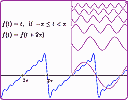 |
Here's an interactive graph that allows you to explore the concepts behind the Fourier Series. |
2. Christmas
(a) An engineer's view of Santa Claus
 |
Here's a fun mathematical analysis of Santa's frantic dash around the world every Christmas Eve. |
(b) 12 Days of Christmas
Each year at this time, my article The Twelve Days of Christmas – How Many Presents? has many readers.
3. Most popular articles of 2012
One of the joys of writing a newsletter is getting a lot of appreciative feedback. Another is to see which articles you enjoyed the most, and to use this information to plan future Newsletters.
Here are the most popular IntMath Newsletter items during 2012 (based on traffic).
Resources & math articles
- Free Textbooks in Mathematics (no longer available)
- Modelling Fish Stocks
- Absolute value of a complex number
- Today is e-day
- Wolfram Education Portal
- Desmos Graphing Calculator
Interactives
- Interactive Ellipse Graphs
- Radius of Curvature interactive graph
- Conic Sections 3-D interactive
- Differentiation interactive graphs
- Biorhythm graphs
Videos
4. Looking ahead - 2013
Here are a few things coming up for 2013.
(a) 2013 is year of Math of Planet Earth
The aim of Mathematics of Planet Earth 2013 is to examine the role mathematical sciences play in the challenges facing our planet and our civilization. As they say:
More than 100 scientific societies, universities, research institutes, and organizations all over the world have banded together to dedicate 2013 as a special year for the Mathematics of Planet Earth.
The site has articles about using mathematical models to eradicate disease, the Equation of Time and How does GPS work?
(b) Free online Calculus course starts 7th Jan
Another MOOC (massively online open course) starts 7th January 2013. This time it is an Introduction to Calculus.
The instructor is Robert Ghrist from the University of Pennsylvania. I like where they say the course will have "an emphasis on the conceptual over the computational".
These MOOCs are quite an experience. The last one I joined was Keith Devlin's course on Mathematical Thinking. There were over 60,000 of us involved in that course.
See Calculus: Single Variable for more information and to sign up.
5. Math puzzles
Answer for last puzzle: The puzzle in the last IntMath Newsletter concerned adding fractions. The correct answer was 2475. Those who were correct and showed correct working were: Miguel, John Cherpak, Colin Fraser, Devanie, Thomas A. Buckley, Yeoh Kiat Boon, Guido, Nicos, Tomas, Vasu, Arun, Tom Barrett, Rosa, Ronak (who also included a C program routine), Dineth, and Lachezar.
New puzzle: If n is an even positive integer, how many positive integer solutions are there for 2x + y + z = n? (Express your answer in terms of n).
Leave your responses here.
6. Friday math movie: The mathematics of history
 |
What's the connection between verbs, math and hip hop? |
7. Final thought - Treating others
It's that time when many of us reflect on the past year, and make plans (and resolutions) for the coming one.
The final thought for 2012 is quite global, but can also relate to math learning and the instructor-learner relationship. It's also a good thing to keep in mind for all the interactions we have with those around us.
Each major religion has some suggestions on how we should treat others, known generally as the Golden Rule.
Buddhism: "Hurt not others with that which pains yourself."
Judaism & Christianity: "You shall love your neighbor as yourself."
Islam: "As you would have people do to you, do to them; and what you dislike to be done to you, don't do to them."
Hinduism: "One should always treat others as they themselves wish to be treated."
Sikhism: Recognize all of mankind as a single caste of humanity and accept all humans as your equals.
Zoroastrianism: "Whatever is disagreeable to yourself, do not do unto others."
Confucianism: "What you do not want done to yourself, do not do to others."
In summary, "Treat people the way you'd like to be treated".
The IntMath Newsletter will return in mid-Januray. Enjoy your Christmas and/or New Year holiday season.
Until next time, enjoy whatever you learn.
See the 18 Comments below.
18 Dec 2012 at 5:31 pm [Comment permalink]
Please note: I will publish all the Puzzle responses at one go, after a period of a few weeks.
18 Dec 2012 at 6:16 pm [Comment permalink]
Sikhism: Recognize all of mankind as a single caste of humanity and accept all humans as your equals.
18 Dec 2012 at 7:29 pm [Comment permalink]
@JSH - Thanks for the addition about Sikhism. I have added it to the article.
18 Dec 2012 at 10:10 pm [Comment permalink]
Answers of this equation 2x+y+z=n are:
x=1,2,3,...n/2
y=2,4,6,...n
z=2,4,6,...n
18 Dec 2012 at 11:40 pm [Comment permalink]
If n is an even positive integer, how many positive integer solutions are there for 2x + y + z = n? (Express your answer in terms of n).
Answer:
When n=2 there are 4 posibilities:(3+1) for x, y, z (0,0,2), (0,2,0), (0,1,1), (1,0,0). In the case n=4 there are 9 posibilities 3+5+1=9. For n=6 is 3+5+7+1=16 and so on. The general formula for n the number of combinatios is n(1+n/4)+1
19 Dec 2012 at 6:35 pm [Comment permalink]
Number of positive integer solutions for
x are Sx = n*(n+1)/2
y are Sy = n*(n+1)
z are Sz = n*(n+1)
20 Dec 2012 at 1:03 am [Comment permalink]
First examine the #sol for a few values of n
x y z if n=1 ----> #Sol=2
0 0 1
0 1 0
etc...
Then we see:
n=1 #Sol=2
2<= n <=3 #Sol=4 and 6 =2n
4<= n <=5 #Sol=9 and 12 =3n-3
6<= n <=7 #Sol=16 and 20 =4n-8
etc...
20 Dec 2012 at 1:04 am [Comment permalink]
We see that #Sol=(A+1)n - B
with A'=n/2. If A'=int then A=A'; if not A=A'-0.5
and B is the sum of the upper limits of n until the previous
interval.This is an arithmetic progression with v=2
B= S{A-1}-1 = A(1+A-1) -1 = A^2-1
So: #Sol = (A+1)n - (A^2-1) is the answer
F.i Let
n=5 ---> A=2--->#Sol= 3n - 3 = 12
20 Dec 2012 at 2:11 am [Comment permalink]
HI,
My name is Dineth and I have answered your many puzzles (most of the time correctly and with reasoning). Today, I'll just leave a comment.
If you give a real life problems, mostly word problems if can, blend with some interesting story, I think it's rather better than answers to an equation.
This is my personal opinion and it's only a friendly suggestion. I love your work. keep it up.
Thanks,
20 Dec 2012 at 7:20 am [Comment permalink]
@Dineth - Thanks for your suggestion. I also tend to prefer "real life" problems, but every now and then it's also good to solve various kinds of problems. I'll keep it in mind for the future, of course.
Thanks for your kind feedback - happy holidays to you!
20 Dec 2012 at 9:34 am [Comment permalink]
The number of possible variations of x,y and z
to return any specified relevant value of n is
(n/2-1)^2
Satisfying the puzzle conditions:
If n is an even positive integer, how many positive integer solutions are there for 2x + y + z = n?
A bolts and nuts approach, being ignorant of any more
useful mathematical method, has developed as follows:-
All possible values of x, y, and z to yield
n = 2, 0 combinations,(write down all the permutations).
n = 4, 1
n = 6, 4
n = 8, 9
n =10, 16
n =12, 25
This can be continued until n = infinity (an even infinity!)
So how can the number of combinations, on the right of the table, be derived from the corresponding value of n?
By inspection this easily evolves as,
(n/2-1)^2 = Answer to this Puzzle.
Example, for 2x + y + z to equal say 1000,
there are (1000/2-1)^2 = 249001 possible
values for x,y and z.
20 Dec 2012 at 10:08 am [Comment permalink]
I must confess that I had to go through direct enumeration. Not being too skilled in number theory, I resorted to my faithful servant, Mathematica, and constructed a table of (2 x, y, z) for the first 100 integral values of x, the first 200 integral values of y and the first 200 integral values of z, i.e,. a table with 100 x 200 x 200 = 4,000,000 rows. Then, for each even n from 2 to 12 I counted the number of rows for which 2 x + y + z = n, for n = 2, 4, 6,.... This took an amazingly long time (about 85 seconds in a moderately fast computer), and the answer for the first 12 values of n is (n/2 - 1 ) squared. The proof is left for a more competent mathematician
27 Dec 2012 at 11:36 pm [Comment permalink]
I salute you regarding your effort to make everyone fearless of Mathematics.
Please can't we always get solutions to previous quiz (workings inclusive) to make your positive aim more achievable.
Thanks.
28 Dec 2012 at 8:48 am [Comment permalink]
@Alayande: Thank you for your kind comments.
In each Newsletter I link back to the previous Puzzle question (for those who missed it), and have a link to the supplied solutions (and I include the final answer if it is simple). I also indicate which people had correct working, so it's easy for you to see a variety of correct solutions.
31 Dec 2012 at 8:51 am [Comment permalink]
Required to find the number of solutions in positive integers to 2X + Y + Z = N where N is an even integer. The answer to be in terms of N.
It can be readily established that there is no solution for N =2. By substitution it can be shown that for N = 4 there is one solution.Similarly for N = 6 there are 4 solutions and for N = 8 there are 9 solutions etc. These results can be tabulated as follows:
1 2 3 4 Solution No
4 6 8 10 Value of N
1 4 9 16 No of Solutions
By inspection the no. of solutions is the square of the solution no.
The solution No = (N-2)/2.
Therefore the number of solutions =( (n-2)/2)^2 for all N > 3 and n/2 an integer.
8 Jan 2013 at 11:24 pm [Comment permalink]
since 2x+y+z=n,where n is even no.,y and z can be zero and x can be a factor of n..but y and z should be positive integers.Now y+z=m,where m is also an even integer.m can take total of (n/2-1)values.so y+z=m will have m-1 solutions..so solutions will have the form:
sigma of(i*(ni-1)) from 1 to (n/2-1)=
(n(n-1)(n-2))/24-(n-2)/2.
9 Jan 2013 at 10:44 pm [Comment permalink]
2x+y+z=n
x can take values from 0 to n/2
consider one value of x = r, for that r,
y+z=n-2r, for each r, y can take 0 to n-2r and corresponding
value of z is fixed.
so total solution =sigma from 0 to n/2 of n-2r = n/2((n/2)+1)
8 Feb 2013 at 10:49 am [Comment permalink]
i learned a lot... thanks