8. Radius of Curvature
By M. Bourne
We can draw a circle that closely fits nearby points on a local section of a curve, as follows.
Application of Radius of Curvature

When engineers design train tracks, they need to ensure the curvature of the track will be safe and provide a comfortable ride for the given speed of the trains. [Image source].

We say the curve and the circle osculate (which means "to kiss"), since the 2 curves have the same tangent and curvature at the point where they meet.
The radius of curvature of the curve at a particular point is defined as the radius of the approximating circle. This radius changes as we move along the curve.
How do we find this changing radius of curvature?
The formula for the radius of curvature at any point x for the curve y = f(x) is given by:
`text(Radius of curvature)` `=([1+((dy)/(dx))^2]^(3//2))/(|(d^2y)/(dx^2)|)`
Proof
The curvature of a given curve at a particular point is the curvature of the approximating circle at that point.
The curvature depends on the radius - the smaller the radius, the greater the curvature (approaching a point at the extreme) and the larger the radius, the smaller the curvature. (A very large approximating circle means the curve is almost a straight line at that point.)
The radius of curvature R is simply the reciprocal of the curvature, K. That is,
`R = 1/K`
So we'll proceed to find the curvature first, then the radius will just be the reciprocal of that curvature.
Let P and `P_1` be 2 points on a curve, "very close" together, as shown.
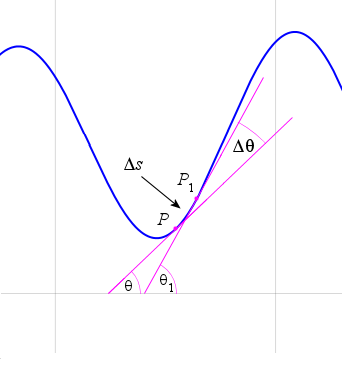
`Delta s` is the length of the arc `PP_1`.
`Delta theta` is the angle turned by the tangent line as it moves from P to `P_1`.
The curvature of the arc from P to `P_1` is given by
`(Delta theta)/(Delta s)`
Now, the curvature K at point P is given by:
`K=lim_(Delta theta->0)(Delta theta)/(Delta s) = (d theta)/(ds)`
We now need to find `(d theta)/(ds)` and we use the Chain Rule: ` (d theta)/(ds) = (d theta)/(dx)dx/(ds)`
Note that `tan\ theta=dy/dx`, so `theta=arctan(dy/dx)`
Returning to our formula, ` (d theta)/(dx)= d/(dx)arctan ((dy)/(dx))`
In the Differentiation of Transcendental Functions chapter we'll learn the derivative of `y=arctan\ u`, where `u=f(x)`, is given by `(dy)/(dx)=((du)/(dx))/(1+u^2)`
With `u= arctan ((dy)/(dx))` we differentiate as follows:
` (d theta)/(dx)= d/(dx)arctan ((dy)/(dx))`
`=(d/dx(dy/dx))/(1+(dy/dx)^2)`
`=((d^2y)/dx^2)/(1+(dy/dx)^2)`
We also need `dx/(ds)`, which is given by:
`(dx)/(ds)=1/((ds)/(dx))=1/sqrt(1+(dy/dx)^2)`
Putting it all together gives us the formula for curvature, `K`:
`K= (d theta)/(ds)=((d^2y)/(dx^2))/[1+(dy/dx)^2]^(3/2)`
Now the radius of curvature is just the reciprocal of this expression, that is:
`R= [1+(dy/dx)^2]^(3text(/)2)/((d^2y)/(dx^2))`
Of course, the radius needs to be positive, so we take the absolute value of the denominator (bottom) of the fraction.
`R= [1+(dy/dx)^2]^(3text(/)2)/(|(d^2y)/(dx^2)|)`
Example 1
Need Graph Paper?
Find the radius of curvature for the cubic
y = 2x3 − x + 3
at the point x = 1.
Answer
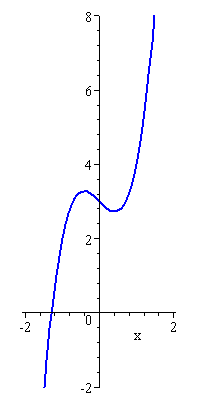
First, let's draw the graph and see what the question means.
y = 2x3 − x + 3
I have used equal scaling along the 2 axes (so that later, when I draw the circle, it will not have an elliptical shape).
Now, to find the radius of curvature, we need:
`(dy)/(dx)=6x^2-1`
And then
`((dy)/(dx))^2=(6x^2-1)^2`
`=36x^4-12x^2+1`
So now we are ready to substitute into the formula to give us the radius at any point x:
`R=[1+(dy/dx)^2]^(3"/"2)/(|(d^2y)/(dx^2)|)`
`=[1+36x^4-12x^2+1]^(3//2)/{|12x|}`
`=[36x^4-12x^2+2]^(3//2)/{|12x|}`
Now to find the radius of curvature at the required point x = 1, we substitute:
`[[36x^4-12x^2+2]^(3//2)/{|12x|}]_(x=1)` `=11.04787562`
To show what we have done, let's look at the graph of the curve (blue) with the approximating circle (dark red) overlaid. The circle is a good approximation for the curve at (1, 4).
We can show that the center of the approximating circle is `(−9.8, 6.17)`.
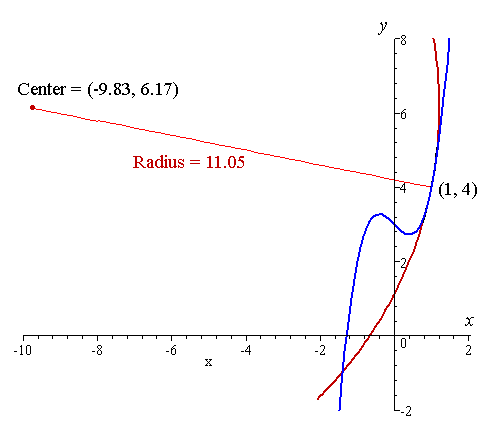
How did I find that center?
We know the length of the radius shown in the diagram (`11.05` units).
We know 1 point on that radius line, `(1,4)`, and we need to find the one at the other end, the center. Let's call it (x1, y1).
We're going to set up 2 equations using these 2 unknowns.
We know that
`(dy)/(dx)=6x^2-1`
So the slope of the tangent at `x = 1` is
6(1)2 − 1 = 5.
Now, the slope of the normal (the line at right angles to the tangent at the point of contact) is −1/5. (See Tangents and Normals.)
So we can use the formula y − y1 = m(x − x1) and the known slope `-1/5` and point `(1, 4)` to find the equation of the line containing the radius as follows:
y − 4 = (−1/5) (x − 1), which gives:
`y = −x/5 + 21/5`
The unknown point (x1, y1) lies on this line, so we can say
`y_1=-(x_1)/5+21/5`
Next, we use the distance formula:
`sqrt((x_2-x_1)^2+(y_2-y_1)^2)=r`
We know the distance r (since it is the radius), and one of our points is (1,4), and using our expression connecting x1 and y1, we can solve these simultaneously as:
`sqrt((1-x_1)^2+[4-(21/5-1/5x_1)]^2)` `=11.04787562`
This is one equation in one unknown, which after some algebra gives us
x1 = − 9.833 (and another positive solution which doesn't apply here)
Substituting this back into `y_1=-(x_1)/5+21/5` gives
y1 = 6.167
So the center of the circle is `(−9.8, 6.17)`.
Exploration
In the following interactive graph you can explore what "changing radius of curvature" means.
Slowly drag the point "P" around the curve to see the changing radius of curvature (segment CP). It works best if you use a left-right motion - don't worry about following the up-down of the graph.
You'll notice at the point of inflexion there is interesting behavior. The circle changes from being below the curve to above (when moving left to right). When we are right on the point of inflexion, what does the circle become?
Example 2
[This example was supplied by a reader.]
We have a curve which is defined by data points and we don't know the function for this data. How can we find the radius of curvature?
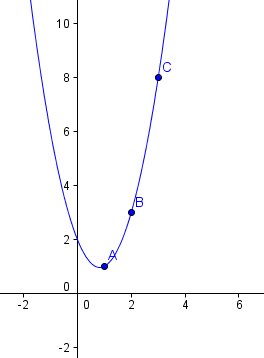
We take any 3 data points to illustrate ways of solving this. I chose the points (1, 1), (2, 3) and (3,8).
We'll do this in 3 different ways, just for fun (and for learning about how different math approaches can be used)!
Method 1: Approximation Using a Parabolic Fit and Calculus Methods
Answer
The graph connecting the generic data points `(1, 1)`, `(2, 3)` and `(3, 8)` is as follows.
One way of finding the radius of curvature is to find the (unique) parabola passing through these 3 points. Parabolas are excellent for approximating curves in a local region. (See more on Parabolas.)
We proceed as follows. In general, a parabola has the form:
y = ax2 + bx + c
Substituting our given points (1, 1), (2, 3) and (3, 8) into the general form of the parabola gives us 3 equations in 3 unknowns:
1 = a + b + c
3 = 4a + 2b + c
8 = 9a + 3b + c
Solving this set of 3 simultaneous equations gives us:
a = 1.5
b = −2.5
c = 2
So the parabola passing through the points `(1, 1), (2, 3)` and `(3, 8)` is
y = 1.5x2 − 2.5x + 2
We see this parabola passes through each of the 3 points:
Using this as our function (which we can only do in this local region for the original data points), we apply the formula for the radius of curvature:
`text(Radius of curvature)` `=([1+((dy)/(dx))^2]^(3//2))/|(d^2y)/(dx^2)|`
We need to find the first and second derivatives and evaluate them at the center point `(2, 3)`.
`(dy)/(dx)=3x-2.5`
At `x = 2` (the middle of our 3 points), `dy/dx = 3.5`
Now for the second derivative:
`(d^2y)/(dx^2)=3`
So the radius of curvature at the middle point (2, 3) is:
` [1+(dy/dx)^2]^(3text(/)2)/(|(d^2y)/(dx^2)|)=[1+(3.5)^2]^(3//2)/3`
`=16.08`
So we've found a parabola that approximates our function for the local area near our data points. Then we found the radius of curvature - that is, the radius of a circle that "fits" our curve near our data points.
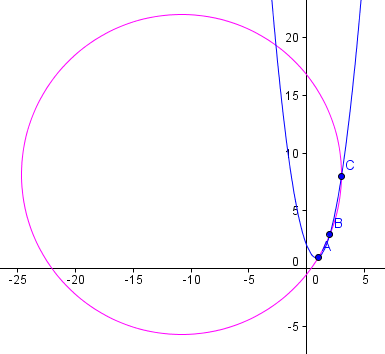
Here are the 3 data points, the parabola we found, and the circle indicating the curvature for the given 3 points. It has radius `16.08`.
Method 2: Using Linear Approximations and Calculus Methods
Answer
We can approximate the value of `(dy)/(dx)` at the middle point `(2,3)` of our 3 points as follows.
The slope of the line joining `(1, 1)` and `(2, 3)` is given by:
`m_1=(Deltay)/(Deltax)=2/1=2`
The slope of the line joining `(2, 3)` and `(3,8)` is given by:
`m_2=(Deltay)/(Deltax)=5/1=5`
We "average" these slopes to find a crude value for `(dy)/(dx)`:
`"Average slope"=(2+5)/2=3.5~~(dy)/(dx)`
Now for the slope of the slope (i.e. the second derivative). We find the change in slope m divided by the change in x for the interval x = 1.5 to x = 2.5 (which are the mid-points of our 2 lines joining the 3 given points):
`"Slope of slope"=(Deltam)/(Deltax)=(5-2)/1` `=3~~(d^2y)/(dx^2)`
Interestingly, these approximate values are exactly the same as our parabola approximation above.
Substituting into our radius of curvature formula, we obtain the same value as for Method 1:
`[1+(dy/dx)^2]^(3text(/)2)/(|(d^2y)/(dx^2)|)=[1+(3.5)^2]^(3//2)/3`
`=16.08`
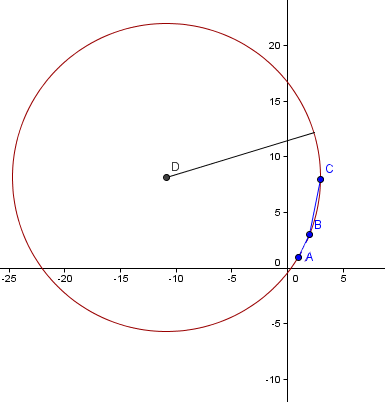
Checking our answer, we can see that the (dark red) approximating circle (center D, with radius `16.08`) passes quite closely through our data points. It may be possible to improve on this by taking weighted averages to get more appropriate values for the first and second derivatives.
Of course, my reader would need to do the same process for every set of 3 adjacent data points. He was writing a computer program to do this, so it would not be so tedious.
Method 3: Finding the Radius of the Circle through our 3 Points
Answer
This is an exact method for finding the required radius of curvature. We'll actually find the equation of the circle passing through the 3 points.
In general, the x-value for the center of the circle passing through 3 points A (x1, y1), B (x2, y2), C (x3, y3), joined by lines with slopes m1 and m2 is given by:
`x_c=(m_1m_2(y_1-y_3)+m_2(x_1+x_2)-m_1(x_2+x_3))/(2(m_2-m_1)`
(The above formula is based on finding the intersection of the perpendicular bisectors of the 2 lines joining the 3 points, as follows.)
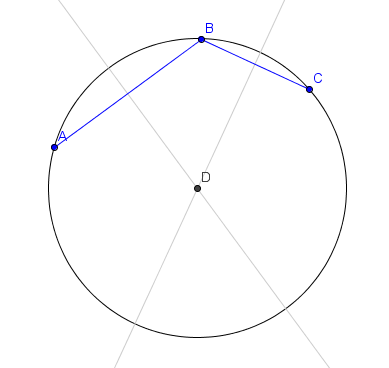
So for our given data points, we have:
`x_c =((2)(5)(1-8)+(5)(1+2)-(2)(2+3))/(2(5-2))`
`=-10.833`
(We found the values for m1 and m2 in Method 2, above.)
Now to find the y-value for center of the circle. The formula for the first perpendicular bisector is given by:
`y_("Perp")` `=- 1/m_1(x-(x_1+x_2)/2)+(y_1+y_2)/2`
So for our data points, we can obtain the y-value for the center of the circle by substituting the known values, as follows:
`y_c` `=-1/2(-10.833-(1+2)/2)+(1+3)/2` `=8.1665`
So the center of the circle passing through the points `(1, 1), (2, 3)` and `(3, 8)` is given by `(-10.83, 8.17)`.
Finally, we can find the radius by simply finding the distance between the center of the circle and any one of the points on the circle. I have chosen `(1,1)`:
`text(Radius) = sqrt((x_2-x_1)^2+(y_2-y_1)^2`
`=sqrt((1-(-10.833))^2+(1-8.1665)^2)`
`=13.834`
[See more on Distance Formula.]
So the radius of curvature for the 3 points `(1, 1), (2, 3)` and `(3, 8)` is `13.83`, when finding the actual circle passing through the 3 points.
Our answer is slightly different to the answers obtained by using a parabolic model and linear approximations.