7. Applied Maximum and Minimum Problems
by M. Bourne
The process of finding maximum or minimum values is called optimisation. We are trying to do things like maximise the profit in a company, or minimise the costs, or find the least amount of material to make a particular object.
These are very important in the world of industry.
Example 1
The daily profit, P, of an oil refinery is given by
P = 8x − 0.02x2,
where x is the number of barrels of oil refined. How many barrels will give maximum profit and what is the maximum profit?
Answer
The profit is a max (or min) if `(dP)/(dx)=0`.
`(dP)/(dx)=8-0.04x`
`=0`
when
`x=8/0.04=200`
Is it a maximum?
`(d^2 P)/(dx^2) = -0.04 < 0` for all x, so we have a maximum.
When `x = 200`, `P = $800`.
So if the company refines `200` barrels per day, the maximum profit of `$800` is reached.
Graph of `P=8x-0.02x^2`.
The maximum point, `(200, 800)` is indicated on the graph with a magenta dot.
[Go here to see another way to find the maximum or minimum value of a parabola.]
Example 2
A rectangular storage area is to be constructed along the side of a tall building. A security fence is required along the remaining 3 sides of the area. What is the maximum area that can be enclosed with `800\ "m"` of fencing?
Answer
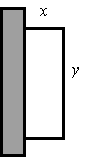
The area is `A = xy`
We know `2x + y = 800` so `y = 800 − 2x`
So the area is A = x(800 − 2x) = 800x − 2x2
To maximise the area, find when `(dA)/dx = 0`
`(dA)/(dx)=800-4x=0`
when
` x=200`
Is it a maximum?
`(d^2A)/(dx^2)=-4<0\ "for all"\ x`
So it is a maximum.
So the maximum area occurs when `x = 200`, `y = 400` and that area is:
A = 200 × 400 = 80 000 m2 = 8 ha
Example 3
[This problem was presented for discussion earlier in the Differentiation introduction.]
A box with a square base has no top. If 64 cm2 of material is used, what is the maximum possible volume for the box?
Answer
The net for this box would be:
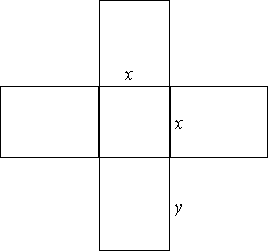
The volume of the box is V = x2y
We are told that the surface area of the box is 64 cm2. The area of the base of the box is x2 and the area of each side is xy, so the area of the base plus the area of the 4 sides is given by:
x2 + 4xy = 64 cm2
Solving for y gives:
`y=(64-x^2)/(4x)=16/x-x/4`
So the volume can be rewritten:
`V=x^2y`
`=x^2(16/x-x/4)`
`=16x-x^3/4`
Now
`(dV)/(dx)=16-(3x^2)/4`
and this is zero when
`x=+- 8/sqrt(3) ~~ 4.62`
(Note: The negative case has no practical meaning.)
Is it a maximum?
`(d^2V)/(dx^2)=-(3x)/2`
and this is negative when x is positive. So it is a MAX.
So the dimensions of the box are:
Base 4.62 cm × 4.62 cm and sides 2.31 cm.
The maximum possible volume is
V = 4.62 × 4.62 × 2.31 ≈ 49.3 cm3
Check: Area of material:
x2 + 4xy = 21.3 + 4 × 4.62 × 2.31 = 64
Checks OK.