IntMath Newsletter: Bezier curves interactive, KinectMath, puzzles
By Murray Bourne, 17 Jan 2013
17 Jan 2013
In this Newsletter:
1. Interactive Bezier Curve Graphs
2. Kinect Math
3. IntMath polls
4. HOTmaths revisited
5. Math puzzles
6. Friday math movie
7. Final thought - Questions for learning
Happy New Year everyone!
In case you missed it, 2013 is year of Mathematics of Planet Earth. Events will include public lectures like "The challenge of sustainability and the promise of mathematics" by Princeton University professor Simon Levin in Melbourne, Australia on 29th Jan 2013.
In math class we should be making better use of math students' time and energy to plan for a more sustainable, and happier future.
1. Interactive Bezier Curve Graphs
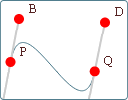 |
Here's an interactive graph where you can explore straight lines, parabolas, cubics and Bezier curves. You'll find it towards the bottom of this Math of Vector Art page. |
2. Kinect Math
 |
Many students prefer learning via hands-on activities. Kinect Math is an interesting approach using Microsoft's Kinect. Students interact with various graphs and other math concepts using their hands. See some videos about it here: KinectMath - A Kinesthetic Learning Experience (no longer available) |
3. IntMath Poll: Math homework per week
The latest poll asked readers about the amount of math homework they do per week during semester. Here are the results:
More than 6 hours
36%
Between 2 and 4 hours
16%
Between 1 and 2 hours
14%
Between 4 and 6 hours
12%
Less than 1 hour
12%
None
9%
Total votes: 2,900.
The surprise here is that over 1/5 of respondents do one hour or less For most math courses, this would be inadequate.
New poll: The latest poll asks readers whether it's important to know the history of each math topic. You can respond on any page in IntMath.
4. HOTmaths revisited
 |
HOTmaths is an interesting online math resource. I take another look after a few years. Do you use it? How do you find it? |
5. Math puzzles
The puzzle in the last IntMath Newsletter involved finding the number of possible positive integer solutions for a given equation.
Correct answers with reasoning were given by Thomas A Buckley and Tom Barrett.
Tomas Garza fired up Mathematica, produced a 100 x 200 x 200 item table, and then used brute-force counting (which took over a minute) to find the correct rows, and from there deduced the correct answer.
A systematic approach is to consider the smallest value of y + z which occurs when y = z = 1, and if so, 2x is then n − 2. Then we can let x = 1, 2, 3 ... (n − 2)/2. Then y + z = n − 2, n − 4, n − 6, ... to which there are n − 3, n − 5, n − 7, ... solutions in positive integers. We then use the sum of an arithmetic progression formula to obtain the solution (n − 2)2/2.
New puzzle: A certain bathtub with the plug in and the tap on will fill at a uniform rate in 12 minutes. The bath will empty with the plug out at a uniform rate in 15 minutes. How long will it take to fill the bathtub if the plug is out, the tap is on, and it was originally empty?
Leave your responses here.
6. Friday math movie: Teach statistics before calculus!
 |
This short talk argues that people should know about probability and statistics before calculus. Do you agree with him? |
7. Final thought: Questions for learning
Many students do not maximize their learning outcomes. If we turn up for class with no idea what's going to happen, we just make it harder for ourselves.
Here are some things to think about before your next math class.
How have I prepared for class today? (Revised last week's key points? Understood what the formulas mean? Done the homework? Looked over what we are going to do today?)
What's the best way for me to prepare for a class like this one? (Sharing ideas with others can be a good way to pick up tips.)
What questions do I have? (If you have a good clear list of things you want to find out or understand better, it helps focus your learning. Sharing questions and answers with classmates can help to understand what is going on.)
Why did I get these exam questions wrong? (Many students just worry about the exam grade, but don't put effort into understanding what went wrong. Talking through the common errors is a good way not to repeat them.)
What do I need to do to avoid missing questions like these on the next exam? (Thinking about this will also help you focus in class. If your tests are mutliple choice, try hiding the choices before doing the problem. Too many students try to work backwards from the most likely correct answer!)
(Based on Teaching Metacognition to Improve Student Learning)
Until next time, enjoy whatever you learn.
See the 15 Comments below.
17 Jan 2013 at 3:36 pm [Comment permalink]
1 bath filled per 12 mins
0.083333333 water in / min
1 bath emptied per 15 mins
0.066666667 water out / min
0.016666667 NET / min
1/0.016666667 = 60
60 mins = 1 hour
17 Jan 2013 at 7:53 pm [Comment permalink]
In response to the Jan 17, 2013 newsletter puzzle: if the tub fills in 12 min., then 1/12 of the tub fills per minute. Likewise, if teh tub empties in 15 min., then 1/15 of the tub empties per minute. Using these unit rates, we can write the equation: (1/12)t - (1/15)t = 1 , where t represents time in minutes. Solving this equation requires getting a common denominator and subtracting the two fractions leaving us with: (1/60)t = 1. Then we solve and find that t = 60 minutes or 1 hour.
17 Jan 2013 at 9:43 pm [Comment permalink]
Happy new year!
With the tap on in 1 min the 1/12 of the tub will be filled and with the plug out the 1/15 of the tub will be evacuated. So in 1 min it remains 1/12-1/15=1/60 of water. The tub will be totally filled in 60*1/60 = 1 hour.
17 Jan 2013 at 11:13 pm [Comment permalink]
V = liters in bathtub full
Time to fill = Tf = 12 min.
Rate to fill = Rf = V/Tf = V/12 (liters per min)
V= Rf x Tf
Time to empty = Te = 15 min.
Rate to empty = Re = V/Te = V/15 (liters per min)
V= Re x Te
Rnew = Rf – Re = V/12 – V/15 = 15V/180 – 12V/180 = 3V/180 = V/60
V = Rnew x Tnew
Solve for Tnew: Tnew = V/Rnew = 60 minutes!
18 Jan 2013 at 2:39 am [Comment permalink]
Answer to bathtub math puzzle
If the fill time is 12 minutes and empty time is 15 minutes
if we use an arbitrary number of 100 gal to stand for the full quantity
then
the fill rate is 100/12 = 8.333333 gal/min
the empty rate is 100/15 = (-)6.666666 gal/min
therefore the net gain into the tub is
8.333333 - 6.666666 = 1.6666666 gal/min
then to fill the 100 gals (again this is arbitrary)
takes 100 / 1.66666 = 60 minutes
therefore it will take 60 minutes to fill the tub
18 Jan 2013 at 1:43 pm [Comment permalink]
It takes 1 Hour to fill the bath.
1. Let v = Volume of bath. ( Litres, Gals, or whatever units of capacity).
Then the rate of Volume gain = v/12 units/min,
and the rate of Volume loss = v/15 units/min.
So the rate of Volume gain is the difference = (v/12 - v/15) = v/60 units/min
Clearly if it is gaining 1/60 of it's Volume each min
it will take 60 mins or 1 hour to fill = Answer
2. If a general equation is required;
Minutes to fill
= product/ difference
= 15 x 12/( 15-12) = 60 mins = 1 Hour = Answer.
Some may identify this as a variation of a two resistors in parallel formula.
18 Jan 2013 at 8:01 pm [Comment permalink]
The tap fills the bathtub with the plug in at a rate of 1/12 of the bathtub per minute and the drain empties it at a rate of 1/15 of the bathtub per minute. The difference between these (i.e. how much the bath fills each minute with the plug left out) is 1/12 - 1/15 = 1/60. So with the plug out the bath fills at a rate of one 60th of the bathtub per minute, i.e. it takes 60 minutes to fill the bathtub.
19 Jan 2013 at 7:07 pm [Comment permalink]
v= volume of bath tub
t= time for filling of bath tub
rate of bath tub filling=v/12
rate of bath tub empty=v/15
t*v/12-t*v/15=v
t=60min.=1 hr.
21 Jan 2013 at 4:31 pm [Comment permalink]
x/12-x/15=1
x = 60 min.
23 Jan 2013 at 12:18 am [Comment permalink]
Let us assume volume of the bathtub is X. as it fills in 12 minutes, the rate is X/12 per minute. As it will empty in 15 minutes when plugged-out, its rate is X/15. When tap is on and plug is out, the difference is (X/12)-(X/15) = X/60. (As this is a positive number, it fills with a rate of 1/60 per minute) Therefore, the time taken to fill it completely is an hour. (60 minutes)
27 Jan 2013 at 11:54 pm [Comment permalink]
To fill the tank with water with water let in and and not let out = 1/12 mins
To empty with only plug out on = 1/15 mins
both on at the same time the rate of filling = 1/12 - 1/ 15 =1/60
so fill it you take minimum of 60 minutes after which it will overflow and and also get drained through the plug out.
28 Jan 2013 at 11:08 pm [Comment permalink]
solution:
(1/12 - 1/15)d = 1
(1/60)d = 1
d = 1*60
d = 60
It will take 60 minutes to fill.
29 Jan 2013 at 5:29 pm [Comment permalink]
Hello Murray sahib,
A good afternoon to you !
I have not yet had a good look at what you presented to us in this news letter. So this is not a comment on any of your articles.
One of my "articles" whose material I clobbered together , has found a posting on one of the Indian web-sites on whose forum I am a member .
Perhaps it would interest you too ! ?
It here :
~~~~~~~~~~~~~~~~
Ramanujan’s LETTER
Dated : Madras, 16th January 1913
Dear Sir,
I beg to introduce myself to you as a clerk in the Accounts Department of the Port Trust at Madras on a salary of pounds twenty per annum. I am now about 23 years of age.
I have had no university education but I have undergone the ordinary school course. After leaving school I have been employing the spare time at my disposal to work at Mathematics.
I have not trodden through the conventional regular course which is followed in a University course, but I am striking out a new path for myself. I have made a special investigation of divergent series in general , and the results I get are termed by the local mathematicians as “ startling”.
………… I request you to go through the enclosed papers . Being poor, if you are convinced that there is anything of value I would like to have my theorems published.
I have not given the actual investigations nor the expressions that I get but I have indicated the lines on which I proceed.
Being inexperienced, I would very highly value any advice you give me.
Requesting to be excused for the trouble I give you.
I remain,
Dear Sir,
Yours truly,
S. Ramanujan
~~~~~~~~~~~~~~~~~~~~~~~~~
{ the * enclosed papers* went on for nine pages. Within these 9 papers , ordinary English virtually disappeared , giving way to the symbolic language of algebra, trigonometry and calculus. There were theorems in number theory, theorems devoted to evaluating definite integrals, theorems on the summation of infinite series, and much more~~~ fifty of them all together.
They were the work of “a rare flower of exotic genius “}
By the year 1912 , Ramanujan was convinced that , in effect , his mathematical output was just too big for Indian mathematicians. He should try to get the sympathetic hearing from European mathematicians.
So, in the late 1912 he started writing letters to some of the leading mathematicians at Cambridge University ; including with letters samples of his work.
He wrote to H.F. Baker , president of the London Mathematical Society.
Baker said : ' No '.
Ramanujan wrote to E. W. Hobson , a famous mathematician and Fellow of the Royal Society .
Hobson too said no. !!
On January 16, 1913 , Ramanujan wrote to Professor G. H. Hardy of the Cambridge University. Hardy was 35, a generation younger than the other men. He was already a famous mathematician .
Hardy’s was the newer voice in Pure Mathematics that was buzzing in mathematical circles.
“Could Hardy help “ , asked Ramanujan.
And Hardy said , YES
There followed a series of correspondence between the two . Subsequently Hardy made up his mind to bring Ramanujan to England.
As a result, Ramanujan landed in the UK on the ship
* S. S. NEVASA* on April 14, 1914
From then on, Hardy took steps to advance Ramanujans works. He acknowledged his genius and nurtured it.
Hardy's personal ratings of mathematicians : " suppose that we rate mathematicians on the basis of pure talent on a scale from 0 to 100, Hardy gave himself a score of 25, J.E. Littlewood 30, David Hilbert 80 and Ramanujan 100.'"
Hardy wrote : " ----His letters contained the bare statement of about 120 theorems. Several of them were known already, others were not. Of these, some I could prove (after harder work than I had expected) while others fairly blew me away. I had never seen the like! Only a mathematician of the highest class could have written them. They had to be true, for if they were not, no one would have the imagination to invent them---"
"____In his favourite topics, like infinite series and continued fractions, he had no equal this century. His insight into algebraic formulae, often (and unusually) brought about by considering numerical examples, was truly amazing---"
References :
1) " Ramanujan " by G.H Hardy
2) Wikipedia : " Srinivasa Ramanujan "
3) " The Man Who Knew Infinity " by Robert Kanigel
~~~~~~~~~~~~~~~~^^^^^^^^^^^^^^
Regards
ahmed
30 Jan 2013 at 11:50 pm [Comment permalink]
Very interesting article. I do wonder if Ramanujan had ever met Baker and Hobson after he was recognized by Prof. Hardy and recognized by the world.
To motivate my students to learn Mathematics tell them Ramanujam's story ( including his childhood days).
Thank you Mr. Ahmed for sharing the lettters with us.
Ramesh
19 Feb 2013 at 11:19 am [Comment permalink]
In one minute water left out is (1/12)-(1/15) =(1/60)th of the tank, hence it takes 60 minutes to fill the tank, if the plug is out and tap is on.