Mathematics of Vector Art

[SVG image by GDJ. Source]

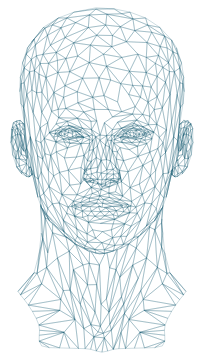
This wireframe image of a human head is an example of a scalable vector graphics (SVG) file. Wireframes are used as the basis for CGI (computer-generated imagery) in videos. The wireframe is mostly made up of triangles.

Vector art is used extensively in the movie and games industries. It consists of a combination of basic mathematical shapes, called primitives, which are described below.

(See some background to this topic here: Vector Art.)

Polygons

A polygon is a many sided figure. The simplest 2-dimensional polygon is the triangle. Here are the first 5 regular polygons (triangle, square, pentagon, hexagon, heptagon).

Of course, we could also use irregular polygons:

The above wireframe face is mostly triangles, but you can find irregular polygons as well.

Circle

The circle is also a common shape used in vector graphics. A circle with radius r has equation:

x² + y² = r²

See The Circle for more information.

Ellipse

We also can make use of the ellipse in vector art. An ellipse with major axis a and minor axis b (assuming the ellipse is longer horizontally) has equation:

`x^2/a^2+y^2/b^2=1`

For more background on this, see The Ellipse.

Bezier Curves

Bezier Curves connect 2 or more points with a smooth curve. We can have either:

a. Linear Bezier Curves

This is simply a straight line passing through 2 points.

We learned before that straight lines can be written in the form

`y = mx + b`

(See more on Straight Lines)

For example, we can join the points `A(1, 4)` and `B(-3, 12)` with the straight line `y = -2x + 6`.

To obtain the equation of this line, I used the formula

y − y₁ = m(x − x₁)

b. Quadratic Bezier Curves

We wish to draw a parabola (or quadratic Bezier curve) through 3 given points `P(1, 2)`, `Q(3, 5)` and `R(5, 4)` as follows

To find the required quadratic, we use the general form of the quadratic and substitute the known values of x and y. (See background on this at The Parabola.)

`y = ax^2+ bx+ c`

Substituting our 3 points gives us:

`2 = a + b + c`

`5 = 9a + 3b + c`

`4 = 25a + 5b + c`

Now we have 3 equations in 3 unknowns, which we can solve using matrices or linear methods. (See Matrices.)

After some algebra, we find that the equation of the required curve is:

`y=-0.5x^2+3.5x-1`

And here is the graph of the required quadratic curve, passing through the 3 given points:

c. Cubic Bezier Curves

We can find a cubic curve passing through 4 given points using the same process that we just did for the quadratic curve above.

For example, if I use the same 3 points `P(1, 2)`, `Q(3, 5)` and `R(5, 4)` as I did for the above example and then add a 4th point `S(6, 10)`, to find the cubic curve passing through these 4 points I need to set up a set of 4 equations in 4 unknowns, using the general cubic:

`y = ax^3+ bx^2+ cx + d`

Solving those resulting 4 simultaneous equations for a, b, c, d (using a computer algebra system) gives me the following cubic curve passing through the 4 points:

`y=0.53x^3-5.3x^2+15.77x-9`

Here is the resulting curve passing through the 4 given points:

Interactive Bezier Curve Graphs

In the following interactive, you can explore the examples given for the 4 types of Bezier Curves mentioned above.

In each case, drag the points and see the effect on the curve. (The equations are greyed out when you drag because once you modify the curve, the equation no longer applies.)

We create vector art using such curves.

Drawing Bezier Curves in a Graphics Program

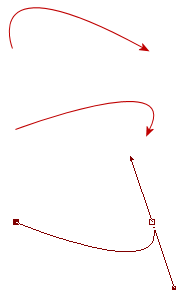
When you use a graphics program to draw Bezier curves, it does all the required mathematics for you in the background.

In the example on the left, I have created 3 vector arrows, which in this case are curves passing through 2 points. In the 3rd one, you can see how it is looks during the creation process, similar to the fourth interactive curve above. I can drag the handles into whatever curve shape I desire.

Later, I can edit the shape of the arrow or resize the vector and there will be no loss of quality. This is very difficult to do with a raster image - you would need to start again and draw the whole thing.