2. Vector Addition (1-dimensional vectors)
Adding 1-dimensional Vectors
I am swimming downstream in a river.

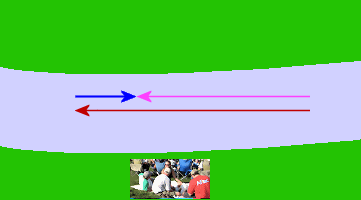
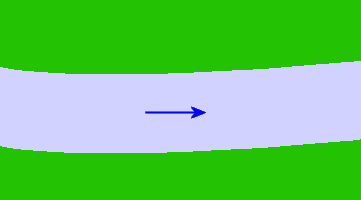
The speed of the river current is 0.25 m/s, as indicated by the length and direction of the blue arrow in the vector diagram.
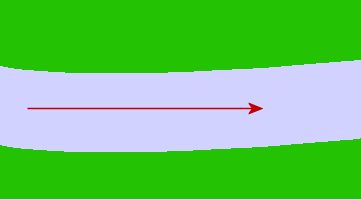
I swim downstream at the rate of 1 m/s, as indicated by the dark red arrow below. (It is `4` times the length of the river current vector, indicating that my swimming velocity is `4` times the velocity of the river current.)
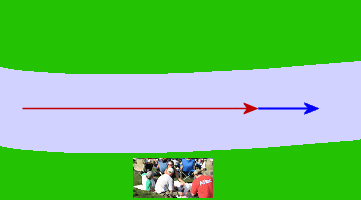
Our friends are on the riverbank watching me swim. They observe that I am moving quite quickly. My velocity is:
1 + 0.25 = 1.25 m/s.
The river is helping me to move quickly relative to the people watching. This is an example of vector addition.
We can show this on our diagram as follows:
The equivalent vector (1.25 m/s downstream) is shown in pink:
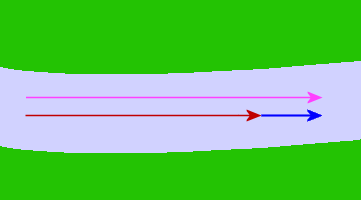
The diagram illustrates the boost that I am getting from the river current and demonstrates my total speed, relative to the riverbank, of:
1 + 0.25 = 1.25 m/s.
The Return Journey (Subtraction of Vectors)
To get back to my friends, I need to swim against the current so my speed relative to the people who are watching me will be less. My velocity relative to the river bank is now:
1 − 0.25 = 0.75 m/s.
The 2 vectors are now acting in opposite directions.
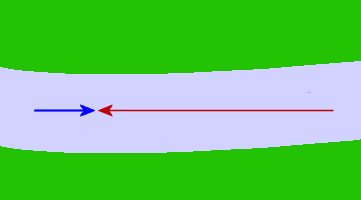
An equivalent way of drawing our 2 vectors is to put the tail of the current vector next to the tip of the swimming vector as follows:
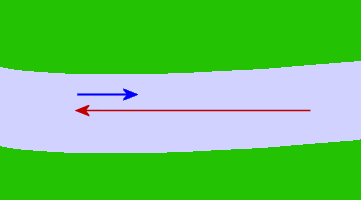
My velocity relative to the people watching (0.75 m/s, upstream) is shown in pink: