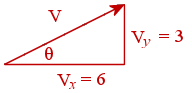3. Vectors in 2 Dimensions

So far we have considered 1-dimensional vectors only.

Now we extend the concept to vectors in 2-dimensions. We can use the familiar x-y coordinate plane to draw our 2-dimensional vectors.

The vector V shown above is a 2-dimensional vector drawn on the x-y plane.

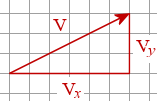
The vector V is acting in 2 different directions simultaneously (to the right and in the up direction). We can see that it has an x-component (`6` units to the right) and a y-component (`3` units up).

Components of Vectors

Reading from the diagram above, the x-component of the vector V is `6` units.

The y-component of the vector V is `3` units.

We can write these vector components using subscripts as follows:

V_x = 6 units

V_y = 3 units

Magnitude of a 2-dimensional Vector

The magnitude of a vector is simply the length of the vector. We can use Pythagoras' Theorem to find the length of the vector V above.

Recall (from Section 1, Vector Concepts) that we write the magnitude of V using the vertical lines notation | V |.

We have:

Magnitude of V

`= | bbV | ` `= sqrt(6^2+ 3^2)` `= sqrt(45)` `= 6.71\ "units"`

Direction of a 2-dimensional Vector

To describe the direction of the vector, we normally use degrees (or radians) from the horizontal, in an anti-clockwise direction.

We use simple trigonometry to find the angle. In the above example, we know the opposite (`3` units) and the adjacent (`6` units) values for the angle (θ) we need.

So we have:

`tan theta=3/6=0.5`

This gives:

θ	= arctan 0.5 = 26.6° (= 0.464 radians)

So our vector has magnitude 6.71 units and direction 26.6° up from the right horizontal axis.