10. Vector Calculus

Rate of Change of Variable Vectors

We saw in Variable Vectors how vectors can vary with time. In this section, we learn how to find the rate of change of such varying vectors.

To find the time rate of change of a vector, we simply differentiate each component.

Example 1

Let's consider the 2-dimensional force vector example from before:

F = (3t² + 5) i + 4t j

The time rate of change of this vector is given by the derivative with respect to t of each component.

`(dbb{text(F)})/dt=6t\ bb{text(i)}+4\ bb{text(j)}`

At time `t = 5`, the rate of change of the vector F is the vector 30 i + 4 j. The units will be N/s.

Example 2

The 3-D acceleration vector we met earlier in Example 2, Variable Vectors was given by

A = (5t) i + (2t + 3) j + (t² + 10) k

The rate of change of this vector is given by differentiating each term, as follows:

`(dbb{text(A)})/dt=5\ bb{text(i)}+2\ bb{text(j)} +2t\ bb{text(k)}`

The units will be m/s³.

At the specific time t = 4 s, the rate of change of the vector will be

5 i + 2 j + 8 k m/s³

Rate of Change of a Position Vector in Elliptical Motion

Next we consider the case when the terminal point of a vector is moving in an ellipse.

Example 3

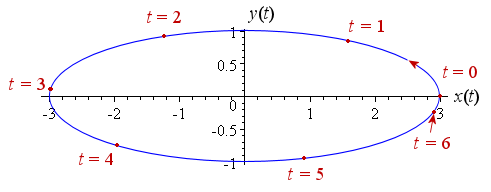
The following vector (units in m) follows such a pattern at time t (units in s):

P = (3 cos t) i + (sin t) j

This expression is based on the expression for a circle , P = (cos t) i + (sin t) j. The 3 in the i term stretches the circle into an ellipse. Of course, the time t is measured in radians, not degrees.

Following is the graph of the motion of the terminal point of the ellipse.

The terminal point starts at t = 0 s at the position `(3, 0)` and proceeds in an anti-clockwise direction. Its position at various times is indicated on the graph.

This idea of a curve being generated as a point moves in time is the same concept as Parametric Equations that we came across before.

The resulting vector has initial point at the origin as above. The vector for the cases t = 0 s (magnitude 3 m, direction horizontal, to the right), t = 1 s and t = 2 s are shown below:

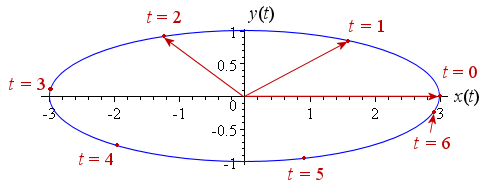
To find the time rate of change of the position vector in elliptical motion, we differentiate the terms as we did earlier.

Since

P = 3 cos t i + sin t j

then

`(dbb{text(P)})/dt=-3\ sint\ bb{text(i)}+cost\ bb{text(j)}`

Note that the magnitude of the vector changes as time goes on because the terminal point is moving around the ellipse.

To find the rate of change at particular times, we substitute in values of t.

At t = 0 s,

rate of change

= 0 i + j = j

Considering our diagram above, this answer makes sense. When the terminal point starts to move, it is in the vertical direction only (no horizontal component is present).

At t = 1 s, we expect a negative horizontal component and a positive vertical component (the terminal point is moving up and to the left at t = 1 s) . Substituting `t = 1` (in radians, of course) gives us:

rate of change

= (-3 sin 1) i + (cos 1) j = -2.52 i + 0.54 j

The x-value is negative and the y-value is positive, as expected.

At t = 6 s, we expect a positive horizontal component (the terminal point is moving to the right) and a positive vertical component (the terminal point is moving up).

rate of change

= (-3 sin 6) i + (cos 6) j = 0.84 i + 0.96 j

Both components are positive, as expected.