4. Adding Vectors (in 2 dimensions)

Let's first have a play. The following interactive applet involves a Cessna that is trying to land on the runway, but the cross-wind is quite strong.

Instructions

You are the pilot. If you have lined up the Cessna properly, you'll be able to land. If not, you need to go around and try again. You can only land towards the north (runway 36, heading towards the top).

Choose your wind direction and away you go. You can steer with the right and left arrow keys on your keyboard. You can pause at any time to see what is going on with the various vectors involved.

On a tablet or smart phone, tilt your screen to steer.

Things to do

• Have a fly around first to get a feel of the controls
• Try to fly due North, or perhaps due East
• Now attempt your landing. The challenge is to put it down exactly in the center of the runway, near the number "36", while flying due North.

Good luck.

Note 1: In navigation (on ships and planes), angles are measured from due north (0° = 360°) in a clockwise direction. So for example, East is 090° and South is 180°.

Note 2: Runway markings do not include the last digit for the runway's direction, so "Runway 36" means aircraft land in the direction 360° and "Runway 18" means 180°.

What Was that All About?

What we did in the Cessna activity was to add vectors in 2 dimensions.

Example - Crosswind Landing

In the activity we were approaching the airport in an aircraft that is flying through the air at 120 kt. We say its airspeed is 120 kt.

(Note: kt = knot, or nautical mile per hour, is the official metric unit for speed in aircraft).

There was a strong Westerly crosswind of 20 kt (as indicated by the windsock).

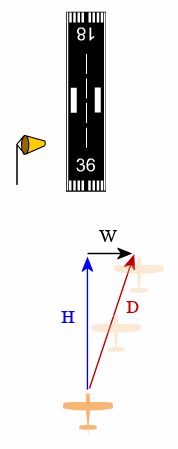
If we point the nose of the aircraft directly at the airport, we will be pushed by the wind away from the landing strip.

In the diagram,

W is the wind vector (in black),

H is the heading of the aircraft (the direction the nose of the aircraft is pointing - in blue) and

D is the resulting direction that the aircraft actually takes across the ground (in red).

Pointing the nose directly at the airport is not a good option. We clearly need to point the nose into the wind so that we go straight to the landing area.

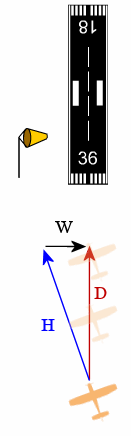
Now the aircraft is pointing into the crosswind, so now we are actually going where we want to go (directly towards the landing area).

What we have seen in this crosswind landing example is addition of vectors. We added the W (wind) vector with the H (heading) vector to give us our resultant vector D (where the aircraft actually goes, relative to the ground).

We could write this as:

D = W + H

Note 1: In flight and marine navigation, North is regarded as 0° = 360° and angles on the compass are measured clockwise. So

90° is East,
180° is South and
270° is West.

Note 2: Actually, a Cessna cannot land if there is a direct crosswind of 20 kt (the usual upper limit is around 15 kt), and most small Cessnas will land at around 70 kt). The figures used in the activity were chosen to make the effect of the crosswind more pronounced.

Adding Vectors Using a Parallelogram

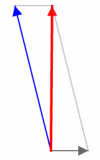
In the applet activity above, you would have noticed a parallelogram of forces that changed with the change in heading of the plane or the wind direction.

The parallelogram is an alternative method to using triangles. If we add the the blue (heading) vector and the black (wind) vector the resultant vector is the red ground direction vector. In the image, the ground direction is due North.

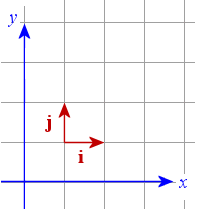
Unit Vectors and Components of a Vector (2-D)

We met the idea of a "unit vector" before in 1. Vector Concepts. We now extend the idea for 2-dimensional vectors.

The diagram shows a unit vector in the x-direction (called vector i) and another in the y-direction (called vector j).

We can write any 2-dimensional vector in terms of the unit vectors i and j.

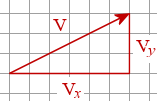
Example

In an earlier example, we had the following vector:

We could write the components of the vector V as follows.

V_x = 6 i

V_y = 3 j

So we can write the vector V using unit vectors as follows:

`"V" = 6\ "i" + 3\ "j"`