5. Dot Product (aka Scalar Product) in 2 Dimensions
Also on this page:
If we have any 2 vectors P and Q, the dot product of P and Q is given by:
P • Q = |P| |Q| cos θ
where
|P| and |Q| are the magnitudes of P and Q respectively, and
θ is the angle between the 2 vectors.
The dot product of the vectors P and Q is also known as the scalar product since it always returns a scalar value.
The term dot product is used here because of the • notation used and because the term "scalar product" is too similar to the term "scalar multiplication" that we learned about earlier.
Example 1
a. Find the dot product of the force vectors F1 = 4 N and F2 = 6 N acting at 40° to each other as in the diagram.
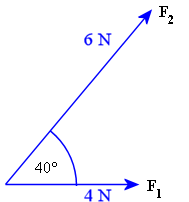
Answer
The dot product is:
F1 • F2
= |F1| |F2| cos θ
= (4)(6) cos 40°
= 18.38 N
b. Find the dot product of the vectors P and Q if |P| = 7 units and |Q| = 5 units and they are acting at right angles to each other.
Answer
The required dot product is:
P • Q
= |P| |Q| cos θ
= 7 × 5 × cos 90°
= 0
The second example illustrates an important point about how scalar products can be used to find out if vectors are acting at right angles, as follows.
Dot Product and Perpendicular Vectors
If 2 vectors act perpendicular to each other, the dot product (ie scalar product) of the 2 vectors has value zero.
This is a useful result when we want to check if 2 vectors are actually acting at right angles.
Dot Products of Unit Vectors
For the unit vectors i (acting in the x-direction) and j (acting in the y-direction), we have the following dot (ie scalar) products (since they are perpendicular to each other):
i • j = j • i = 0
Example 2
What is the value of these 2 dot products:
a. i • i
b. j • j
Answer
(a)
i • i
= | i | | i | cos 0°
= 1 × 1 × 1
= 1
(b)
j • j
= | j | | j | cos 0°
= 1 × 1 × 1
= 1
Alternative Form of the Dot Product
Recall that vectors can be written using scalar products of unit vectors.
If we have 2 vectors P and Q defined as:
P = a i + b j
Q = c i + d j,
where
a, b, c, d are constants;
i is the unit vector in the x-direction; and
j is the unit vector in the y-direction,
then it can be shown that the dot product (scalar product) of P and Q is given by:
P • Q = ac + bd
Answer
For convenience, let vectors P and Q be as shown on the graph. (P is horizontal.)
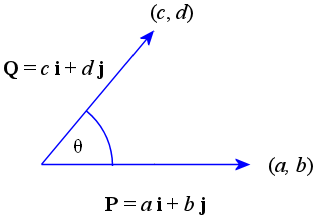
Draw the altitude from vector P to the terminal point (c, d) of Q.
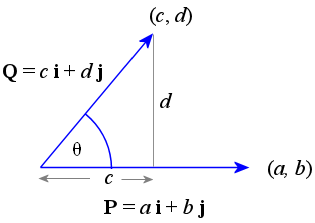
Simple trigonometry gives us:
`cos\ θ = c / | Q |`, so
c = | Q | cos θ
and
`sin\ θ = d / | Q |`, so
d = | Q | sin θ
Since P is horizontal,
a = | P |
b = 0
So
ac + bd
= a | Q | cos θ + 0
= | P | | Q | cos θ
Therefore
P • Q = | P | | Q | cos θ = ac + bd
This result can be generalized for P and Q in any orientation.
Example 3 - Alternative Form of the Dot Product
Find P • Q if
P = 6 i + 5 j and
Q = 2 i − 8 j
Answer
Using the alternative way of finding dot product, we have:
P • Q
= (6 i + 5 j) • (2 i − 8 j)
= (6 × 2) + (5 × -8)
= 12 − 40
= −28
Now we see another use for the dot product − finding the angle between vectors.
Angle Between Two Vectors
We can use the dot product to find the angle between 2 vectors. For the vectors P and Q, the dot product is given by
P • Q = |P| |Q| cos θ
Rearranging this formula we obtain the cosine of the angle between P and Q:
`cos\ theta=(P * Q)/(|P||Q|)`
To find the angle, we just find the inverse cosine of the expression on the right.
So the angle θ between 2 vectors P and Q is given by
`theta=arccos((P * Q)/(|P||Q|))`
Example 4
Find the angle between the vectors P = 3 i − 5 j and Q = 4 i + 6 j.
Answer
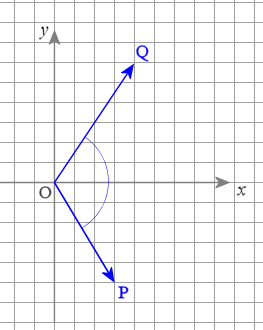
We aim to find angle POQ. We observe that it is an obtuse angle (between 90° and 180°).
We use the formula we just derived:
`theta=arccos((P*Q)/(|P||Q|))`
Taking the numerator first, we have:
P • Q
= (3 i − 5 j) • (4 i + 6 j)
= (3 × 4) + (-5 × 6)
= -18
And now for the denominator (the magnitudes are found using Pythagoras' Theorem):
|P| |Q|
= √(32 + (-5)2) × √(42 + 62)
= 42.048
So
θ = arccos(−18 ÷ 42.048)
Therefore the angle between the vectors P and Q is
θ = 115.3°
This looks a reasonable answer considering the diagram above (which is drawn to scale).