7. Vectors in 3-D Space
On this page...
Magnitude of a 3-D Vector
Adding 3-D Vectors
Dot Product of 3-D Vectors
Direction Cosines
Angle Between Vectors
Application
We saw earlier how to represent 2-dimensional vectors on the x-y plane.
Now we extend the idea to represent 3-dimensional vectors using the x-y-z axes. (See The 3-dimensional Co-ordinate System for background on this).
Example
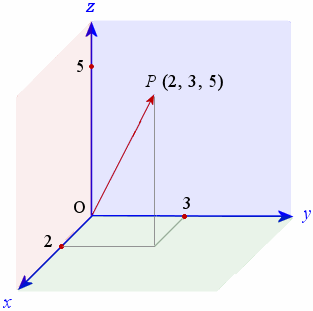
The vector OP has initial point at the origin O (0, 0, 0) and terminal point at P (2, 3, 5). We can draw the vector OP as follows:
Magnitude of a 3-Dimensional Vector
We saw earlier that the distance between 2 points in 3-dimensional space is
`"distance"\ AB = ` `sqrt ((x_2-x_1)^2+ (y_2-y_1)^2+ (z_2-z_1)^2)`
For the vector OP above, the magnitude of the vector is given by:
`| OP | = sqrt(2^2+ 3^2+ 5^2) = 6.16\ "units" `
Adding 3-dimensional Vectors
Earlier we saw how to add 2-dimensional vectors. We now extend the idea for 3-dimensional vectors.
We simply add the i components together, then the j components and finally, the k components.
Example 1

Two anchors are holding a ship in place and their forces acting on the ship are represented by vectors A and B as follows:
A = 2i + 5j − 4k and B = −2i − 3j − 5k
If we were to replace the 2 anchors with 1 single anchor, what vector represents that single vector?
Answer
The problem just requires us to add the vectors to get the single resultant vector.
A + B
= (2 + −2) i + (5 − 3)j + (−4 −5)k
= 0 i + 2 j − 9 k
= 2 j − 9 k
Dot Product of 3-dimensional Vectors
To find the dot product (or scalar product) of 3-dimensional vectors, we just extend the ideas from the dot product in 2 dimensions that we met earlier.
Example 2 - Dot Product Using Magnitude and Angle
Find the dot product of the vectors P and Q given that the angle between the two vectors is 35° and
| P | = 25 units and | Q | = 4 units
Answer
Using our formula from before for dot product:
P • Q = |P| |Q| cos θ
we have:
P • Q
= |P| |Q| cos θ
= 25 × 4 × cos 35°
= 81.92
Example 3 - Dot Product if Vectors are Multiples of Unit Vectors
Find the dot product of the vectors A and B (these come from our anchor example above):
A = 2i + 5j − 4k and B = −2i − 3j − 5k
Answer
A • B
= (2i + 5j − 4k) • (−2i − 3j − 5k)
= (2 × −2) + (5 × −3) + (−4 × −5)
= −4 + −15 + 20
= 1
Direction Cosines
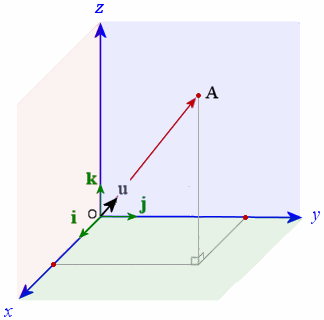
Suppose we have a vector OA with initial point at the origin and terminal point at A.
Suppose also that we have a unit vector in the same direction as OA. (Go here for a reminder on unit vectors).
Let our unit vector be:
u = u1 i + u2 j + u3 k
On the graph, u is the unit vector (in black) pointing in the same direction as vector OA, and i, j, and k (the unit vectors in the x-, y- and z-directions respectively) are marked in green.
We now zoom in on the vector u, and change orientation slightly, as follows:
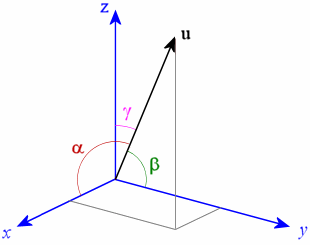
Now, if in the diagram above,
α is the angle between u and the x-axis (in dark red),
β is the angle between u and the y-axis (in green) and
γ is the angle between u and the z-axis (in pink),
then we can use the scalar product and write:
u1
= u • i
= 1 × 1 × cos α
= cos α
u2
= u• j
= 1 × 1 × cos β
= cos β
u3
= u • k
= 1 × 1 × cos γ
= cos γ
So we can write our unit vector u as:
u = cos α i + cos β j + cos γ k
These 3 cosines are called the direction cosines.
Angle Between 3-Dimensional Vectors
Earlier, we saw how to find the angle between 2-dimensional vectors. We use the same formula for 3-dimensional vectors:
`theta=arccos((P * Q)/(|P||Q|))`
Example 4
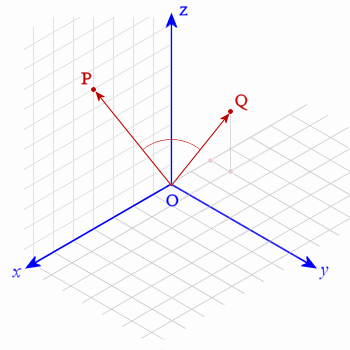
Find the angle between the vectors P = 4i + 0j + 7k and Q = -2i + j + 3k.
Answer
The vectors P and Q are as follows. Vector P is on the x-z plane (note that the y-value for vector P is `0`) , while Q is 'behind' the y-z plane.
Using the formula
`theta=arccos((P*Q)/(|P||Q|))`
we have:
P • Q
= (4 i + 0 j + 7 j) • (−2 i + j + 3 k )
= (4 × −2) + (0 × 1) + (7 × 3)
= 13
And now for the denominator:
`|P||Q|= sqrt (4^2+ (0)^2+ 7^2)` `xxsqrt((-2)^2+1^2+3^2) `
`= sqrt (65)sqrt(14)`
`=30.166\ "units"`
So
θ = arccos(13 ÷ 30.166)
Therefore the angle between the vectors P and Q is
θ = 64.47°
Exercise
Find the angle between the vectors P = 3i + 4j − 7k and Q = -2i + j + 3k.
Answer
Using the formula
`theta=arccos((P*Q)/(|P||Q|))`
we find the dot product first:
P • Q
= (3 i + 4 j − 7 j) • (−2 i + j + 3 k )
= (3 × −2) + (4 × 1) + (−7 × 3)
= −23
And now for the denominator:
|P| |Q|
= √(32 + 42 + (−7) 2) × √((−2)2 + 12 + 32)
= 32.187
So
θ = arccos(−23 ÷ 32.187)
Therefore the angle between the vectors P and Q is
θ = 135.6°
Application
We have a cube ABCO PQRS which has a string along the cube's diagonal B to S and another along the other diagonal C to P
What is the angle between the 2 strings?
Answer
For convenience, we will assume that we have a unit cube (each side has length 1 unit) and we place it such that one corner of the cube is at the origin.
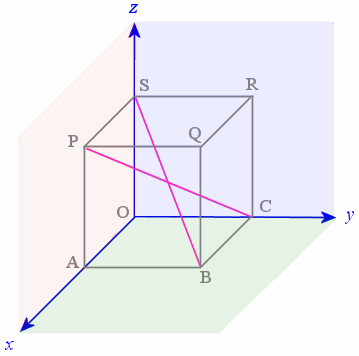
The unit vectors i, j, and k act in the x-, y-, and z-directions respectively. So in our diagram, since we have a unit cube,
OA = i
OC = j
OS = k
From the diagram, we see that to move from B to S, we need to go −1 unit in the x direction, −1 unit in the y-direction and up 1 unit in the z-direction. Since we have a unit cube, we can write:
BS = −i − j + k
and similarly:
CP = i − j + k
The scalar product for the vectors BS and CP is:
BS • CP = |BS| |CP| cos θ
where θ is the angle between BS and CP.
So the angle θ is given by
θ = arccos[ (BS • CP) ÷ ( |BS| |CP| ) ]
Now,
BS • CP
= (−i − j + k) • (i − j + k)
= −1 + 1 + 1
= 1
and
|BS| |CP|
`= sqrt((-1)^2 + (-1)^2 + 1^2)` ` × sqrt(1^2 + (-1)^2 + 1^2)`
`= (sqrt3)(sqrt3)`
= 3
So
`θ = arccos (1/3)`
θ = 70.5°
So the angle between the strings is `70.5°`. (In this situation we assume "angle" refers to the acute angle between the strings.)
Problem Solver
Need help solving a different Graphing problem? Try the Problem Solver.
Disclaimer: IntMath.com does not guarantee the accuracy of results. Problem Solver provided by Mathway.