5. The Ellipse
Later, on this page...
Horizontal major axis
Vertical major axis
Centre other than origin
Why study ellipses?
Orbiting satellites (including the earth revolving around the sun, and the moon revolving around us) trace out elliptical paths.

Earth revolving around the sun
Many buildings and bridges use the ellipse as a pleasing (and strong) shape.

Bridge with elliptical arch
One property of ellipses is that a sound (or any radiation) beginning in one focus of the ellipse will be reflected so it can be heard clearly at the other focus. You can see what this means in the following animation.
Copyright © www.intmath.com
Ellipses with Horizontal Major Axis
Ellipse with horizontal major axis (in blue) and showing the minor axis in magenta color.
The equation for an ellipse with a horizontal major axis is given by:
`x^2/a^2+y^2/b^2=1`
where `a` is the length from the center of the ellipse to the end the major axis, and `b` is the length from the center to the end of the minor axis.
The foci (plural of 'focus') of the ellipse (with horizontal major axis)
`x^2/a^2+y^2/b^2=1`
are at (-c,0) and (c,0), where c is given by:
`c=sqrt(a^2-b^2`
The vertices of an ellipse are at (−a, 0) and (a, 0).
Ellipse showing vertices and foci.
Ellipse as a locus
The ellipse is defined as the locus of a point `(x,y)` which moves so that the sum of its distances from two fixed points (called foci, or focuses) is constant.
We can produce an ellipse by pinning the ends of a piece of string and keeping a pencil tightly within the boundary of the string, as follows.
We start with these 2 foci:

We pin the ends of the string to the foci and begin to draw, holding the string tight:

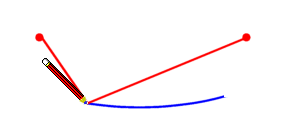
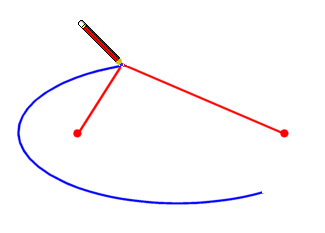
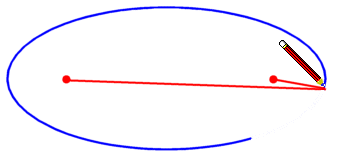
Our complete ellipse is formed:
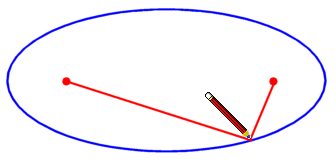
Need Graph Paper?
Example 1 - Ellipse with Horizontal Major Axis
Find the coordinates of the vertices and foci of
`x^2/100+y^2/64=1`
Sketch the curve.
Answer
Here, `a^2= 100`, so `a = ± 10`, so the vertices are at `(-10, 0)` and `(10, 0)`.
Now
`c=sqrt(a^2-b^2)`
`=sqrt(100-64)`
`=sqrt36`
`=6`
So the foci are at `(-6, 0)` and `(6, 0)`.
Ellipse showing vertices and foci.
Ellipse with Vertical Major Axis
Ellipse with vertical major axis (in blue) and minor axis in magenta.
A vertical major axis means the ellipse will have greater height than width.
If the major axis is vertical, then the formula becomes:
`x^2/b^2+y^2/a^2=1`
We always choose our a and b such that a > b. The major axis is always associated with a.
Example 2 - Ellipse with Vertical Major Axis
Find the coordinates of the vertices and foci of
`25x^2+y^2=25`
Sketch the curve.
Answer
`25x^2+y^2=25`
`x^2+(y^2)/25=1`
So `b = 1` and `a = 5`. In this example, the major axis is vertical.
So the vertices are at `(0, -5)` and `(0, 5)`.
To find c, we proceed as before:
`c=sqrt(a^2-b^2)`
`=sqrt(25-1)`
`=sqrt24`
`=4.899`
So the foci are at `(0, -4.9)` and `(0, 4.9)`.
The foci (green dots) are very close to the vertices in this ellipse.
Example 3
Find the equation of the ellipse which has a minor axis of length 8 and a vertex at (0,-5).
Answer
Ellipse with minor axis of length 8 and vertex at (0,-5).
We conclude that `a = 5` and `b = 4`. So the equation of the ellipse is:
`x^2/16+y^2/25=1`
Eccentricity
The eccentricity of an ellipse is a measure of how elongated it is. If the eccentricity approaches value 0, the curve becomes more circular, and if it approaches 1, the ellipse becomes more elongated.
We can calculate the eccentricity using the formula:
`text(eccentricity)=c/a`
Real Example

The Sun
The Earth revolves around the sun in an elliptical orbit, where the sun is at one of the foci. (This was discovered by Keppler in 1610).
The semi-major axis is approximately 149,597,871 km long and it is known that the ratio `c/a` is equal to `1/60`.
(i) What are the greatest and least distances the Earth is from the sun?
(ii) How far from the sun is the other focus?
(The "semi-major axis" means half of the major axis length. In our example, it is (close to) the "average" distance of the sun from the earth, and is also known as one A.U., or "astronomical unit".)
Answer
Part i
The closest we are to the sun is when we are at the vertex closest to the sun (point (150, 0) in the diagram below), and the furthest we are is when we are at the other vertex (point (−150, 0)).
Ellipse with minor axis of length 8 and vertex at (0,-5).
Note: In the graph, I have exaggerated the shape of the elliptical orbit (I squashed it a bit so it looks more elliptical) and the positions for the 2 foci are shown much further apart than they really are.
In the diagram above, units are in millions of kilometers.
The distance a = OA = 149,597,871 is the length of the semi-major axis of our ellipse.
We have assumed that the sun is at the right-hand focus, at the point (c, 0).
The vertices are at A (149 597 871, 0) and B (−149 597 871, 0).
We need to find c, to tell us where the foci are.
`c=a/60`
`=(1\ 495\ 97871)/60`
`=2,493,298`
So the foci are at the points `(-2\ 493\ 298, 0)` and `(2\ 493\ 298, 0).`
The closest we are to the sun is
`a-c= 149\ 597\ 871 − 2\ 493\ 298`
`= 147\ 104\ 573\ "km"
The furthest we are from the sun (distance from B to the sun) is:
`OB+ c = a + c`
`= 149\ 597\ 871 + 2\ 493\ 298`
` = 152 091 169\ "km"`
Part ii
The foci are `2 × c = 2 × 2\ 493\ 298` ` = 4\ 986\ 596` km apart.
The radius of the sun is around `1\ 400\ 000` km, so the 2nd focus is not all that much further out than the surface of the sun.
Our orbit is almost circular. (The eccentricity is very small at `1/60`).
Graphing the Ellipse
Note: To graph the ellipse above, I needed to find b, as follows:
`b=sqrt(a^2-c^2)`
`=sqrt(149\ 597\ 871^2-2\ 493 \ 298^2)`
`=149\ 577\ 092`
Using the formula for an ellipse,
`x^2/a^2+y^2/b^2=1`
the required curve is
`x^2/(149\ 597\ 871^2)+y^2/(149\ 577\ 092^2)=1`
Ellipses with Centre Other Than the Origin
Like the other conics, we can move the ellipse so that its axes are not on the x-axis and y-axis. We do this for convenience when solving certain problems.
For the horizontal major axis case, if we move the intersection of the major and minor axes to the point (h, k), we have:
`((x-h)^2)/a^2+((y-k)^2)/b^2=1`
The ellipse is as follows:
Ellipse with center (h, k).
Example 4
Sketch the ellipse with equation
`((x-1)^2)/25+((y+2)^2)/9=1`
Answer
We first observe that the centre of the ellipse will be at `(1, -2)`. The major axis will have length `10` (since `a = 5`) and the minor axis will be length `6` (since b = 3).
So the sketch is:
Ellipse with center (1,−2).
Conic section: Ellipse
How can we obtain an ellipse from slicing a cone?
We start with a double cone (2 right circular cones placed apex to apex):
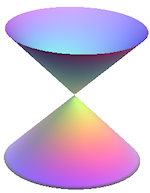
When we slice one of the cones at an angle to the sides of the cone, we get an ellipse, as seen in the view from the top (at right).


