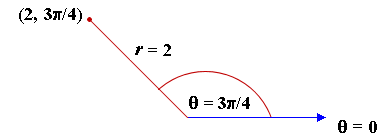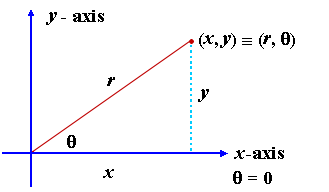7. Polar Coordinates

For certain functions, rectangular coordinates (those using x-axis and y-axis) are very inconvenient. In rectangular coordinates, we describe points as being a certain distance along the x-axis and a certain distance along the y-axis.

But certain functions are very complicated if we use the rectangular coordinate system. Such functions may be much simpler in the polar coordinate system, which allows us to describe and graph certain functions in a very convenient way.

Polar coordinates work in much the same way that we have seen in trigonometry (radians and arc length, where we used r and θ) and in the polar form of complex numbers (where we also saw r and θ).

Vectors also use the same idea. [See more in the Vectors in 2 Dimensions section.]

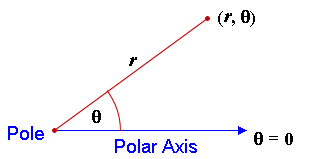
In polar coordinates, we describe points as being a certain distance (r) from the pole (the origin) and at a certain angle (θ) from the positive horizontal axis (called the polar axis).

The coordinates of a point in polar coordinates are written as

(r, θ)

The graph of the point (r, θ) is as follows:

Example 1

The point described in polar coordinates by `(2, (3π)/4)` would look like this:

We use polar graph paper for drawing points in polar coordinates.

NOTE: Angles can be in degrees or radians for polar coordinates.

Example 2

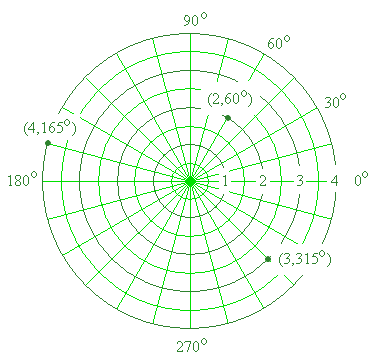
Plot the points on the following polar grid:

a) (2, 60°)
b) (4, 165°)
c) (3, 315°)

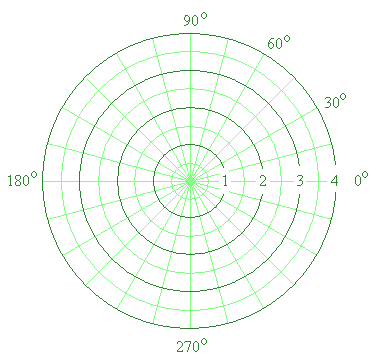
Answer

Converting Polar and Rectangular Coordinates

The conversion from polar to rectangular coordinates is the same idea as converting rectangular form to polar form in complex numbers.

We've created an Polar to Rectangular Calculator that makes converting complex numbers in polar form to rectangular form easy if you don't have a handheld calculator.

We've written an overview for how to convert rectangular and polar forms using various handheld calculators in the complex numbers chapter.

From Pythagoras, we have: r² = x² + y² and basic trigonometry gives us:

`tan\ theta=y/x` x = r cos θ y = r sin θ

So it is the same type of thing that we had with complex numbers.

We can use calculator directly to find the equivalent values.

Example 3

Convert the rectangular coordinates given by `(2.35, -7.81)` into polar coordinates.

Answer

Example 4

Convert the polar coordinates given by `(4.27, 168^@)` into rectangular coordinates.

Answer