Conic sections - summary

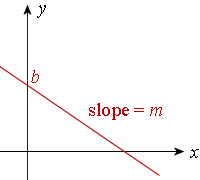
Slope-intercept Form

The equation of a line with slope m and y-intercept b is given by:

y = mx + b

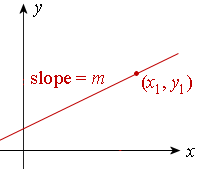
Point-slope form

The equation of a line passing through a point (x₁, y₁) with slope m:

y − y₁ = m(x − x₁)

General Form of a Straight Line

`Ax + By + C = 0`

Conic Section

If we slice the double cone by a plane just touching one edge of the double cone, the intersection is a straight line, as shown.

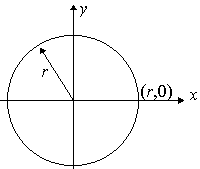
The circle with centre (0, 0) and radius r has the equation:

x² + y² = r²

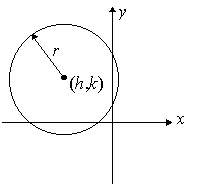
The circle with centre (h, k) and radius r has the equation:

(x − h)² + (y − k)² = r²

General Form of the Circle

An equation which can be written in the following form (with constants D, E, F) represents a circle:

x² + y² + Dx + Ey + F = 0

Conic Section

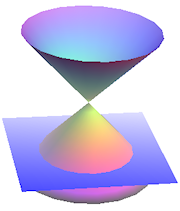
If we slice one of the cones with a plane at right angles to the axis of the cone, the shape formed is a circle.

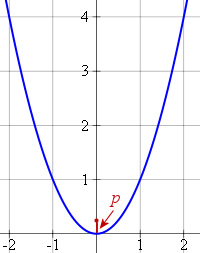
Parabola with Vertical Axis

A parabola with focal distance p has equation:

x² = 4py

In more familiar form, with "y = " on the left, we can write this as:

`y=x^2/(4p)`

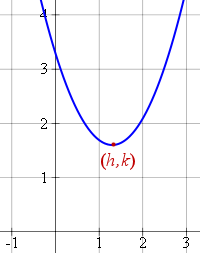
If the axis of a parabola is vertical, and the vertex is at (h, k), we have

(x − h)² = 4p(y − k)

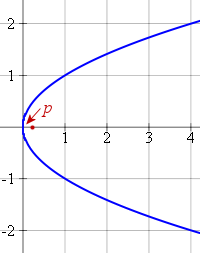
Parabola with Horizontal Axis

In this case, we have the relation:

y² = 4px

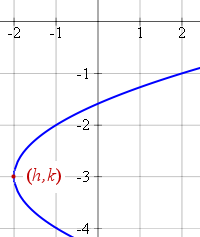
If the axis of a parabola is horizontal, and the vertex is at (h, k), the equation becomes

(y − k)² = 4p(x − h)

Formal Definition

A parabola is the locus of points that are equidistant from a point (the focus) and a line (the directrix).

Conic Section

If we slice a cone parallel to the slant edge of the cone, the resulting shape is a parabola, as shown.

Horizontal Major Axis

The equation for an ellipse with a horizontal major axis and center (0,0) is given by:

`x^2/a^2+y^2/b^2=1`

The foci (plural of 'focus') of the ellipse (with horizontal major axis) are at `(-c,0)` and `(c,0)`, where c is given by:

`c=sqrt(a^2-b^2`

The vertices of an ellipse are at `(-a, 0)` and `(a, 0)`.

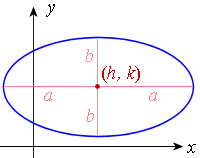
An ellipse with horizontal major axis and with center at (h, k) is given by:

`((x-h)^2)/a^2+((y-k)^2)/b^2=1`

Vertical Major Axis

If the major axis is vertical, then the formula becomes:

`x^2/b^2+y^2/a^2=1`

We always choose our a and b such that a > b.

Formal Definition

An ellipse is the locus of points whereby the sum of the distances from 2 fixed points (the foci) is constant.

Conic Section

When we slice one of the cones at an angle to the sides of the cone, we get an ellipse, as seen in the view from the top (at right).

North-south Opening

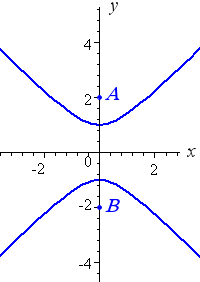
For a north-south opening hyperbola:

`y^2/a^2-x^2/b^2=1`

The slopes of the asymptotes are given by:

`+-a/b`

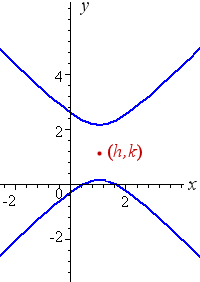
For a "north-south" opening hyperbola with centre (h, k), we have:

`((y-k)^2)/a^2-((x-h)^2)/b^2=1`

East-west Opening

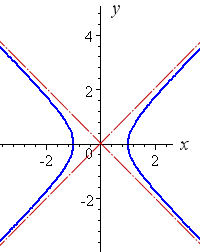
For an east-west opening hyperbola:

`x^2/a^2-y^2/b^2=1`

The slopes of the asymptotes are given by:

`+-b/a`

 

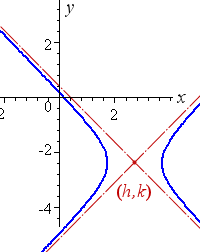
For an "east-west" opening hyperbola with centre (h, k), we have:

`((x-h)^2)/a^2-((y-k)^2)/b^2=1`

Formal Definition

A hyperbola is the locus of points where the difference in the distance to two fixed foci is constant.

General Form of a Hyperbola

`Ax^2 + Bxy + Cy^2 + Dx + Ey + F` ` = 0`

(such that `B^2>4AC`)

Conic Section

When we slice our double cone such that the plane passes througn both cones, we get a hyperbola, as shown.