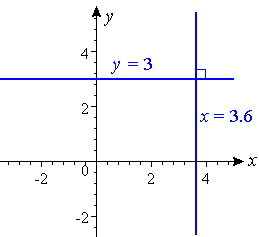Perpendicular Lines
Perpendicular lines have the property that the product of their slopes is −1.
Mathematically, we say if a line has slope m1 and another line has slope m2 then the lines are perpendicular if
m1 × m2= −1
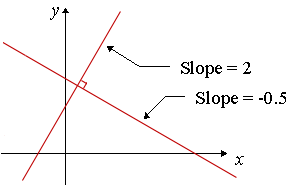
In the example at right, the slopes of the lines are `2` and `-0.5` and we have:
2 × −0.5 = −1
So the lines are perpendicular.
Opposite Reciprocal
Another way of finding the slope of a perpendicular line is to find the opposite reciprocal of the slope of the original line.
In plain English, this means turn the original slope upside down and take the negative.
Interactive graph - perpendicular lines
You can explore the concept of perpendicular lines in the following JSXGraph (it's not a fixed image).
Drag any of the points A, B or C and observe the slopes m1, m2 of the 2 perpendicular lines.
You can move the graph up-down, left-right if you hold down the "Shift" key and then drag the graph.
Sometimes the labels overlap. It can't be helped!
If you get lost, you can always refresh the page.
Special Cases
What if one of the lines is parallel to the y-axis?
For example, the line y = 3 is parallel to the x-axis and has slope `0`. The line x = 3.6 is parallel to the y-axis and has an undefined slope.
The lines are clearly perpendicular, but we cannot find the product of their slopes. In such a case, we cannot draw a conclusion from the product of the slopes, but we can see immediately from the graph that the lines are perpendicular.
The same situation occurs with the x- and y-axes. They are perpendicular, but we cannot calculate the product of the 2 slopes, since the slope of the y-axis is undefined.
Exercise 1
A line L has slope `m = 4`.
a) What is the slope of a line parallel to L?
b) What is the slope of a line perpendicular to L?
Exercise 2
A line passes through (-3, 9) and (4, 4). Another line passes through (9, -1) and (4, -8). Are the lines parallel or perpendicular?
Didn't find what you are looking for on this page? Try search:
Online Algebra Solver
This algebra solver can solve a wide range of math problems. (Please be patient while it loads.)
Go to: Online algebra solver
Ready for a break?
Play a math game.
(Well, not really a math game, but each game was made using math...)
The IntMath Newsletter
Sign up for the free IntMath Newsletter. Get math study tips, information, news and updates each fortnight. Join thousands of satisfied students, teachers and parents!
Share IntMath!
Short URL for this Page
Save typing! You can use this URL to reach this page:
intmath.com/perpendicular
Math Lessons on DVD
Easy to understand math lessons on DVD. See samples before you commit.
More info: Math videos
