IntMath Newsletter: Resources, puzzles, stay relevant
By Murray Bourne, 19 Jun 2012
19 Jun 2012
In this Newsletter:
1. Resource - Data visualization
2. Resource - MathDisk graphing tool
3. IntMath Poll - math software
4. Math puzzles
5. Friday math movies
6. Final thought - Stay relevant
1. Resource - Data visualization
In 2011, the world generated 1.8 zettabytes of data. A "zetta" is 1021, or 1 with 21 zeros behind it.
As we continue to collect and create vast amounts of digital data, we will need more people with the skills to make sense of it all. And there are some great tools in this collection to help with that.
Check out:
I've spent a few hours playing in this collection. Some of my favorites include:
- Google Chart Tools (use Google charts to plot your own data)
- Tangle (a fun tool for creatiing interactive documents)
- Timeline (an interesting way to make sense of recent history)
- GeoCommons (create map-based visualizations)
- Many Eyes (where you could upload your own data and create visualizations, but it's no longer available).
There is a lot to like here, and some great tools that we should be teaching in schools.
2. Resource - MathDisk graphing tool
UPDATE: It seems Mathdisk has disappeared. As it was Flash-based, it's usefulness is now questionable. This is what I said about it:
MathDisk is a new 2-D and 3-D grapher. You can freely create graphs, and free registration allows you to save or share your creations.
There are some interesting pre-built examples in the Gallery, including:
- Spherical Coordinates
- Taylor Polynomial Approximation
MathDisk is Flash-based, so it won't work on iPad or most other tablets. However, it would be good for Interactive Whiteboards.
3. IntMath Poll - math software
The most recent IntMath Poll asked readers:
Do you use math software (like Geogebra, Matlab, Scientific Notebook, Mathematica, or Wolfram|Alpha)?
Results:
I have never used math software: 56%
My teacher and I both use it: 22%
I do but my teacher does not: 14%
My teacher does but I don’t: 9%
I actually ran the same poll question in Nov 2007 and asked it again to see if the situation had improved. The results were almost exactly the same! (In 2007, 54% said they never used math software.)
Of course, I don't know who answered the poll on each occasion. It is quite possible there are no computers available in those respondents' schools. However, as time goes on, more people have access to computers and the use of math software should go up.
This is important because all math students should learn how to use math software. In the workplace they won't be doing pages of algebra using pen and paper - they will use appropriate tools to do it. Math software also changes the math we should learn. A lot of it becomes redundant when we have powerful math tools at our disposal.
Latest poll: The latest poll asks readers about their music tastes while studying math. You can answer on any page in IntMath.com
4. Math puzzles
(a) Solution for last puzzle
Last Newsletter's puzzle was to find the radius of a circular roadway.
The best correct solutions (because they showed clear working) were by one of Aravind's students (complete with a great diagram) and Jegor. Sai Krishna also had the correct answer.
Metric system: One person responded to that puzzle with a strong condemnation of the metric system.
I totally disagree with his assertion that the confusing and user-unfriendly British system (which I grew up with) is in any way better than the simple and easy to use Metric System. Most of the world has already adopted metric measures. It's about time the USA joined the rest of us.
(b) An older, unsolved puzzle - solved at last!
Back in the 27 Oct 2011 Newsletter, I asked the following question, and nobody attempted an answer at the time.
Here is a coded message. Can you figure out what it says?
CGTAOYFUDOORUTNOIRIUNALISUGETT
Reader Jegor was keen to figure it out, so I gave him the hint that the code was built using matrices. He successfully solved it.
Try to solve it yourself before looking at Jegor's correct solution here.
(c) New puzzle
It takes 852 digits to number the pages of a particular book consecutively.
(i) How many pages are there?
(ii) How many times is the digit 7 printed?
Please add your answer here.
5. Friday math movie: Revealing the lost codex of Archimedes
 |
This is the story of how an Archimedes manuscript was recovered from a document that was erased, cut up, written on and painted over. |
6. Final thought - Stay relevant
In this Newsletter, I've talked quite a bit about the importance of moving with the times when it comes to technology in math. I thought the following story of Acu-Math is worth repeating.
For those who have never seen a slide rule, it was used as the main type of mechanical calculator from the 1600s until the 1970s.
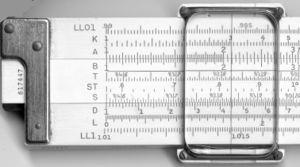
Slide rule. [Image source]
In the 1970s, Acu-Math was one of the world's best-known slide rule manufacturers.
Why have you never heard of Acu-Math? Because they were replaced by companies like Hewlett-Packard and Texas Instruments -- companies that launched the pocket calculator industry.
The problem for Acu-Math and other slide rule manufacturers was that they defined their companies as "manufacturers of slide rules."
But if they'd defined their companies as "manufacturers of tools that help people do mathematical calculations," then they would have constantly been looking for new ways to meet customer needs.
Instead, they defined their company too narrowly.
The result was that when the price of micro-chips dropped low enough to be put into personal calculators, HP and Texas Instruments swept up their customers with new and better tools.
We're in a similar space now. Cheap math software promises to change a lot of what we do in math class, but there is amazing resistance to it. We are using inappropriate and old-fashioned methods for "helping people do mathematical calculations". Are we in danger of becoming the next Acu-Math?
Until next time, enjoy whatever you learn.
See the 22 Comments below.
19 Jun 2012 at 6:06 pm [Comment permalink]
(i) there are (10^852)-1 pages
(ii) 20*(10^850) times the digit 7 will be printed
19 Jun 2012 at 6:57 pm [Comment permalink]
(1)1-9=9pages
10-99=90*2=180pages
100-xxx=y*3=3ypages
3y+180+9=852 so y=221 so xxx-100+1=221 so xxx=320pages
(2) 07,17,27.....97=10 7s
70,71,.. 79 minus one 7 in 77=10 7s
similarly 100-199=20 7s
200-299=20 7s
307, 317=2 7s
total =62 7s
19 Jun 2012 at 10:19 pm [Comment permalink]
Answer : 320 pages
and total 59 occurance of digit 7 is there
20 Jun 2012 at 12:14 am [Comment permalink]
It takes 852 digits to number the pages of a particular book consecutively.
(i) How many pages are there?
Ans.- 320 pages
(ii) How many times is the digit 7 printed?
Ans.- 35 times
20 Jun 2012 at 12:26 am [Comment permalink]
Answer to last puzzle: using the Mathematica functional programming approach it is really quite simple. First, by trial and error, after a few trials (four or five, actually), I get
Total[Length /@ (IntegerDigits /@ Range[320])] = 852,
so the number of pages is 320.
Along the same line of thought, I obtain the frequency of each of the 10 digits 0 - 9:
Count[Flatten[IntegerDigits /@ Range[320]], #] & /@ Range[0, 9]
which gives {62, 172, 163, 83, 62, 62, 62, 62, 62, 62},
so that digit 7 is printed 62 times.
20 Jun 2012 at 2:08 am [Comment permalink]
puzzle c
i) (9 x 1 digit) + (90 x 2 digits)= 189 digits
852-189 = 663 digits
663 / 3 digits = 221 pages
ii) number of 7's:
7 :24 times
20 Jun 2012 at 4:28 am [Comment permalink]
Answer to the puzzle (c) part 1 is
248.
Just imagine a rectangle with all the numbers ( including leading zeros written down in order ). This rectangle is as long as the number itself, and is as wide as the number of digits in the rectangle. If we printed zeros, the number of digits that need to be printed is n*w. ( n - number of pages, w - number if digits in the pages ).
Since we don't print zeros, we remove from this number the number of leading zeros in this list of numbers. This is simply 9, if w=1, (99+9) if w=2, (999+99+9) if w=3 and so on.
So, solve for 852 = n*w - (9+99). Guessing, w=2, gives the answer of 248.
20 Jun 2012 at 6:09 am [Comment permalink]
New puzzle
It takes 852 digits to number the pages of a particular book consecutively.
(i) How many pages are there?
(ii) How many times is the digit 7 printed?
Answer
(i) There are 320 pages.
(ii) The digit 7 is printed 62 times.
20 Jun 2012 at 8:32 am [Comment permalink]
(i) Number of pages
9 Pages 1 to 9 requires 9 digits
90 ,, 10 to 99 ,, 180 ,,
Digits remaining to be used
= 852 -( 9+ 180)
= 663
Next pages from 100 inclusive , each requiring 3 digits
663/3 = 221 pages
Total pages = 9 + 90 + 221 = 320 = Answer (i)
(ii) Number of 7's digit
No of 7,s in the Tens Units
Pages 1 to 9 0 1
,, 10 to 99 10 9
,, 100 to 320 20 22
Total number of 7,s = 10 + 20 + 1 + 9 + 22 = 62
,, 100 to 320
20 Jun 2012 at 9:44 pm [Comment permalink]
It takes 852 digits to number the pages of a particular book consecutively.
(i) How many pages are there?
In the first 9 pages, 1 to 9, nine digits are used
In the next 90 pages, 10 to 99, 180 digits are used
After that, three digits are used for each page.
852 - (9 + 180) = 663
663 / 3 = 221
221 + 99 = 320 pages
(ii) How many times is the digit 7 printed?
Between 1 and 100 there are 10 numbers ending in 7 and 10 numbers beginning with 7. That is 20 copies of "7". The same is true for the 100's, and 200's. So far, that is 60 copies. Between 300 and 320, there are only 2 more, 307, and 317. All of which totals 62 times 7 is printed in 320 pages.
20 Jun 2012 at 10:32 pm [Comment permalink]
Hey Murry I just wanted to say thank you. Im a 57 year old dude who went back to school at 51 ( I retired but wasnt dead yet)and found your site out of desperation. School is over but your site has continued to enrich my life, Thanks. Tim Mallon
21 Jun 2012 at 3:22 am [Comment permalink]
page 1 - 9 -> 2 digits/page -> 18 pages
page 10 -> 3 digits/page -> 3 pages
page 11 - 99 -> 4 digits/page -> 356
page 100 -> 5 digits/page -> 5
page 101 - 999 -> 6 digits/page -> 5394
start at 852 digits and work your way up through the pages by subtracting the above values to calculate amount of pages with 6 digits
(852 - 18 - 3 - 356 - 5)/6 = 80
add all pages = 9 + 1 + 89 + 1 + 80 = 180
21 Jun 2012 at 6:55 am [Comment permalink]
pages 1 to 9 : 9 digits #7 : 1
pages 10 to 99 : 180 digits --- total : 189 #7 :10
pages100 to199 : 300 digits --- total : 489 #7 :11
pages200 to299 : 300 digits --- total : 789 #7 :11
pages300 to319 : 60 digits --- total : 849 #7 : 2
pages320 to322 : 3 digits --- total : 852
So book has 322 pages and 35 x digit 7
21 Jun 2012 at 8:51 am [Comment permalink]
(a) We begin by noting the different types of pages: pages containing one digit, two digits, and three digits.
Pages 1 through 9 (9 pages, or 1 * 9 total digits) each occupy one of the 852 digits.
Pages 10 through 99 (90 pages, or 2 * 90 total digits) each occupy two of the 852 digits.
Pages 100 through 999 (900 pages, or 3 * 900 total digits) each occupy three of the 852 digits; however, logic indicates that there cannot be 999 consecutively numbered pages (beginning at 1) such that only 852 digits are used to number the pages. Therefore, we must determine how many three-digit pages there are in the book (let n represent this).
Notice the form of the 'total digit' products; each has the form: (# of digits)(# of pages requiring said number of digits):
1 * 9 = (1 digit)(9 pages requiring 1 digit)
2 * 90 = (2 digits)(90 pages requiring 2 digits)
3 * n = (3 digits)(n pages requiring 3 digits)
These products represent the number of digits that are being used for 1-, 2-, and 3-digit pages. Summating these products gives 852 digits:
9 + 180 + 3n = 852
3n = 663
n = 221
Therefore, there are 221 pages requiring three digits. When we add to this the nine pages requiring one digit and the ninety pages requiring two digits, we get:
9 + 90 + 221 = 320 total pages.
Hence, there are 320 pages in the book.
Check: 1 * 9 + 2 * 90 + 3 * 221 = 852 total digits
(b) In this part, it is not tedious to list all the pages with which a seven is associated.
1-digit pages: page 7 (1 total page)
2-digit pages: pages 17, 27, 37, 47, 57, 67, 77, 87, and 97 (9 total pages)
3-digit pages up to page 300: pages 107, 117, 127, 137, 147, ... 197; 207, 217, 227, 237, 247, ..., 297 (20 total pages)
3-digit pages between 301 and 320: 307, 317 (2 total pages)
Summating the totals, we get 1 + 9 + 20 + 2 = 32 pages with which a 7 is associated. Remember that the question is not about the number of pages in which seven appears, but rather the frequency at which seven appears. This sum (32)does not account for pages 77, 177, and 277, wherein seven is used twice; thus, we add three to the thirty-two 'seven-associated pages' to obtain 35 'seven frequencies'.
Hence, the number seven is printed 35 times.
21 Jun 2012 at 8:58 am [Comment permalink]
My apologies:
I neglected to add 70, 71, 72, 73, 74, 75, 76, 78, 79, and 170, 171, 172, 173, 174, 175, 176, 178, 179, and 270, 271, 272, 273, 274, 275, 276, 278, 279, giving 27 additional times where seven appears.
Thus, add 27 to 35 to obtain 62 'seven frequencies'.
Hence, the number seven is printed 62 times.
21 Jun 2012 at 9:03 am [Comment permalink]
This solution assumes that the consecutive page numbering beings at page 1.
23 Jun 2012 at 11:27 pm [Comment permalink]
Dear Sir,
The reasons for teachers' resistance to the cheap or any type of software are (i) they are not ready to learn anything new as technology makes the teachers look redundant (ii) it is not easy to understand the use of software (iii) most importantly, it is difficult to look for the most appropriate software for the concept the teacher wishes to teach.
2 Jul 2012 at 12:34 am [Comment permalink]
320 pages
4 Jul 2012 at 3:50 pm [Comment permalink]
There are 320 pages. Single digit pages = 9, equivalent to 9 digits. Two digit pages = 90(99-9):90*2= 180 digits. Three digits = [852 -(9+180)] = 663. Three digit pages = 663/3,equivalent to 221 pages. Therefore total pages = 9 + 90 + 221 = 320. There are 62 sevens printed.-----------------
4 Jul 2012 at 4:02 pm [Comment permalink]
@Tim Mallon: You're welcome and I'm glad you find the IntMath Newsletter useful. There are lots of "mature" people here who have come back to math in later life. Welcome!
4 Jul 2012 at 8:45 pm [Comment permalink]
(i)327 pages
(ii)62 times
27 Sep 2012 at 1:49 am [Comment permalink]
320 pages
7 repeats 62 times