IntMath Newsletter: Fish, brain games
By Murray Bourne, 29 May 2012
29 May 2012
In this Newsletter:
1. Modeling fish stocks
2. National Geographic - memory game and brain interactive
3. Scope of the IntMath Newsletter
4. Math puzzles
5. Friday math movies
6. Final thought - Try!
1. Modeling fish stocks
 |
How can we use math to save collapsing fish stocks? Mathematical modeling is the key. This is an important real-life application of math. |
2. National Geographic - memory game and brain interactive
I came across these on the National Geographic site recently.
Memory game (this is an interesting twist on the normal memory games you've played before)
Brain interactive (this allows you to see what happens in the brain when we form memories)
3. Scope of the IntMath Newsletter
When people subscribe to the IntMath Newlsetter, they can indicate topics they would like me to cover.
I now have (literally) thousands of topic requests, and it would take several lifetimes to get through them all! Of course, I choose the topics which are most often requested.
The scope of topics in the Newsletter will generally follow the scope of the IntMath.com site. That is, basic number and algebra, through matrices, logarithms, trigonometry, to calculus (including Fourier Series and Laplace Transform).
That's already a very broad scope!
4. Math puzzles
The answer to the math puzzle in the last Newsletter was 2πr. The best answers were by Sheldon, Guido and Tomas, because they showed reasons for their correct answers.
Latest puzzle: We are designing an East-West roadway which has a curve consisting of the arcs of 2 identical circles as shown. The straight portions are 900 m apart, and the width of the curved portion is 1200 m. The straight portions of road are tangent to the circles, and the arcs themselves have a common tangent where they meet.
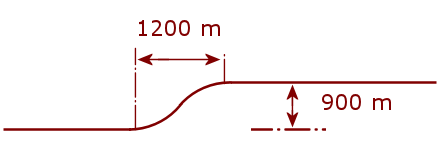
What is the radius of the 2 circles?
You can reply here in the comments.
6. Friday math movie
 |
Hans Rosling on Religions and babies Does religion have an impact on human fertility? Hans Rosling always gives an energetic and thought-provoking presentation. |
7. Final thought - Try!
Many math students give up because they feel it's all too hard. This is a shame, because often it only takes a little bit of reading, or trying a few easier problems, or thinking about the big picture and then insight can occur. (I love those "ahhh - got it!" moments.)
Ralph Waldo Emerson, American writer and lecturer, influenced later ideals of freedom and individualization in the US. He could have been talking to math students when he wrote:
Neither you nor the world knows what you can do until you have tried. [Ralph Waldo Emerson]
Until next time, enjoy whatever you learn.
See the 19 Comments below.
29 May 2012 at 11:13 pm [Comment permalink]
answer is -468.75mts..by pythagores theorem
30 May 2012 at 4:39 am [Comment permalink]
For your math puzzles, is it possible to show the solution to the said puzzle?
I enjoy reading the newsletters. Glad to have suscribed.
30 May 2012 at 4:32 pm [Comment permalink]
This weeks newletter is very interesting. Keep up the good work
31 May 2012 at 8:34 pm [Comment permalink]
Math Text Best-seller
Leonardo of Pisa in twelve-O-two
did something grand
few others could do.
He wrote about math,
from east and from west
and made it quite clear to those who were stressed
doing transactions on fingers and toes
that methods in math could soon fix their woes.
Buyers and sellers and children though small
could finally use math to answer the call
to buy and to sell; crunch numbers with ease
think algebraically; calculate fees.
Without Fibonacci, as he later was called,
our world built on numbers would surely have stalled.
Janine Schaub
September 2011
Hi Murray: I thought this poem might be appropriate for one of your newsletters. Please quote my blog if you use it. Janineschaubpoetry.wordpress.com
31 May 2012 at 8:43 pm [Comment permalink]
Dear Murray Bourne -- I believe the radius of each circle is 900 m (miles)/ 2 = 450 m (miles). I prefer not to use the Napoleonic French metric system which was forced on the European countries at gun point, cannon point, or sword point against their will by Napoleon Boneparte, the fat little thug, and his army. Not only that, but the meter itself is in error. U.S. NASA satellite measurements have determined unequivically that the distance from the North Pole to the equator through a meridian through Paris, France as determined by the French scientists in the late 18th century was 2000 meters too many. The distance was supposed to have been 10,000,000 meters, but in fact is 10,002,000 meters. Therefore the current meter is to short! Check it out. President Thomas Jefferson rightfully rejected the metric system for the United States because for navigation purposes it was worthless -- the British Engineering System (aka U.S. Customery Units) contains intrinsically the unit of Mean Solar Time, and is by far the most superior system.
31 May 2012 at 8:48 pm [Comment permalink]
Hi Janine.
What a great poem! Thanks a lot for sharing. I'll feature it in a future Newsletter.
31 May 2012 at 8:58 pm [Comment permalink]
My solution to puzzle
We have a circle of radius R and center at (0, 450 - R), with known point (600, 0)
(x - a)^2 + (y - b)^2 = R^2
x^2 + (y + R - 450)^2 = R^2
600^2 + R^2 -900R + 202500 = R^2
900R = 562500
R = 625
Radius of circles is 625 m
Thanks,
Jegor
31 May 2012 at 9:00 pm [Comment permalink]
@Ruby: The solutions for the puzzles are provided by readers. In each following Newsletter, I point out the correct answer and the best solutions.
1 Jun 2012 at 2:32 pm [Comment permalink]
I am also wondering what's the solution to CGTAOYFUDOORUTNOIRIUNALISUGETT puzzle, from this newsletter. You suspended puzzles after this one, so solution was never published.
Thanks,
Jegor
1 Jun 2012 at 3:55 pm [Comment permalink]
Dear Sir:
I think the answer to the "two circle" problem is exceedingly and obviously simple. The answer is obvious: it is 900 m / 2. Please show me how that is incorrect if you believe my answer is incorrect.
1 Jun 2012 at 5:54 pm [Comment permalink]
@Jegor: The puzzles are there for readers to answer 🙂
However, I'll give a hint for that puzzle - it involved matrices.
1 Jun 2012 at 6:16 pm [Comment permalink]
Hello,
I used your puzzle in our group, just to start a technical discussion. I got lot of answers, but one student gave me the solution as well as an image. Here it is (click to see full-size):
Regards,
Aravind,
2 Jun 2012 at 12:25 pm [Comment permalink]
Dear sir,
The answer for the math puzzle can be easily derived from the pythagorean theorem that radius is 625m.
3 Jun 2012 at 11:30 am [Comment permalink]
Thanx for the post ,it was realy helpful ,if only we culd get it every week.
18 Jun 2012 at 11:43 am [Comment permalink]
The answer to the problem MATHS PUZZLE of serial No. 4 is the radius is 750 units.because the perpendicular to the common tangent of the the two radii terminating at the two perpendiculars drawn from the end points of 1200 units line is equal to 2r. Forming a right angled triangle with 1200, 960 and the hypotenuse as 2r, we get from the pythogoras formula the following. (2r)^2= (900)^2+(1200)^2 from which, resolving for "r"we get r=750 units. Please correct if the answer is flawed.
20 Jun 2012 at 12:48 am [Comment permalink]
By the way, the condemnation of the metric system has a strong ideological and nationalistic flavor (see Dick's comment in the newsletter). And of course it must be remarked that the meter is currently defined in terms of measurements taken from atomic clocks rather than from the earth's rotation (since 1968). The article in Wikipedia (metric system) offers a good description of the system, which doesn't rely on the actual length of the meter.
Rejection of the metric system in favor of the one still used in the US and the UK reminds me of the Flat Earth Society, whose members stubbornly believe that he Earth is flat.
20 Jun 2012 at 7:33 am [Comment permalink]
For those still interested in the roads problem, I have derived a SIMPLE and UNIVERSAL equation to find the radius
R
= [(W/2)² + (A/2)²]/A . . W = Width, A = Apart
= [(1200/2)² + (900/2)²]/900
= 625m
22 Jun 2012 at 7:39 am [Comment permalink]
My equation for the 'Roads' problem,
further simplified
(W²+A²)/4A
=(1200²+900²)/(4x900)
=625m
22 Jun 2012 at 5:13 pm [Comment permalink]
Dear Murray Bourne --
I messed up on my sulution to the parallel road joined by 2 radii proble. For some reason I had the fixation that the centerline of the two circles was parallel also to the roads -- God only knows why I thought that! Sorry about that. But comment about the Napoleonic French metric system still stands.
I have a problem for all you learned and all-knowing mathematicians out there: Explain analytically and conceptually why a free falling body in a constant gravitational field ALWAYS yields a higher average velocity when computed in the spatial reference frame than in the time reference frame. That also holds in different constant velocity problems as well -- such as what are the average velocities [spatial reference frame vs. time reference frame]of a car that drives from LA to New York at 30 mph but returns from New York to LA at 40 mph?