IntMath Newsletter: Math secrets, TED-ED, puzzles
By Murray Bourne, 07 May 2012
8 May 2012
In this Newsletter:
1. Your math secret
2. TED-ED - Flip your lesson
3. Image conversion project - thank you!
4. Twitter update
5. Math puzzle
6. Friday math movie - The $8 billion iPod
7. Final thought - Apply yourself
1. What's your math secret?
 |
Do you have a secret about your math experiences? Several interesting ones have gone up already. Share yours too! You don't have to reveal your real name. |
2. TED-ED: Flip your Lessons
This one is mostly for teachers, but math students should also find something interesting here.
TED (the place where the world's great thinkers get us to re-evaluate the way we look at the world) recently released TED-ED.
TED-ED is a collection of "Lessons worth sharing". There are lesson plans built around interesting TED talks, and you can either use those lessons, modify them to your own needs, or create a completely new lesson based on the talk.
"Flipping" your lesson involves getting students to learn some things before the actual in-class lesson. This allows students more time to process the concepts during class time, rather than hearing the concepts for the first time. Flipping gained a lot of momentum with the growth of resources like the Khan Academy.
These FAQs explain the TED-ED concept.
Here is the Math Category
There's also a Math in Real Life series of TED talks.
3. Twitter update
There are now over 3000 people following IntMath on Twitter! The 3,000th follower was a design engineer.
There are many good people sharing educational messages and resources there. It's a great place for getting to know people and for sharing interesting finds.
Why don't you join us?
4. Convert images project - thank you!
A big thank you to all those who helped out in the recent IntMath image conversion project. There were a few thousand images converted and now it's all done.
I'm in the process now of removing the old images and replacing them with the new ASCIIMathML-produced, MathJax output equivalents.
You an see some examples of converted images in the math on this page:
Related Rates (calculus)
5. Math puzzles
Several people wrote in to answer the last puzzle about numbers. The correct answers were 41 and 50. Great to see reasons given for the answers!
New Puzzle
Line ABCD is a diameter of a circle whose radius is r. Length AB = BC = CD. Semicircles are drawn on AB and BD to create the shaded figure as shown.
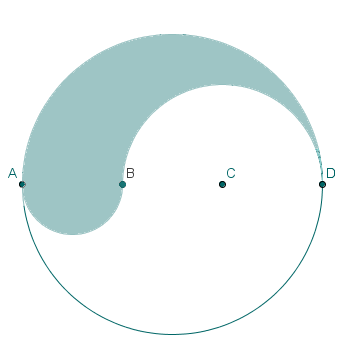
What is the perimeter of the shaded figure?
6. Friday math movie: The $8 billion iPod
 |
Rob Reid gets us to think about how silly the music and movie industries have been regarding copyright. He explains Copyright Math. |
7. Final thought - application
Lee Iacocca, colorful chairman of Chrysler Motors for many years, was named one of the top American CEOs of all time. The following quote could apply to what we do with our math knowledge:
Apply yourself. Get all the education you can, but then, by God, do something. Don't just stand there, make it happen. [Lee Iacocca]
Until next time, enjoy whatever you learn.
See the 14 Comments below.
8 May 2012 at 11:10 am [Comment permalink]
The perimeter is 2*pi*r, where r is the radius of the original circle.
If AB = BC = CD, then since AD is the diameter of the original circle, it is therefore 2r. Therefore AB = BC = CD = (2/3)r.
The semicircle with diameter AB must have circumference
(1/2)*pi*AB = (1/2)*pi*(2/3)*r = 1/3*pi*r.
The semicircle with diameter BD must have circumference
(1/2)*pi*BD = (1/2)*pi*(4/3)*r = 2/3*pi*r (since BD is twice AB).
Finally, the remainder of the shaded figure is the semicircle from A to D (which happens to be half the circumerence of the original circle). Its circumference is (1/2)*pi*AD = (1/2)*pi*(2r) = pi*r.
Adding these three measurements up, we have (1/3)*pi*r + (2/3)*pi*r + pi*r = 2*pi*r.
8 May 2012 at 5:04 pm [Comment permalink]
hey,
for the puzzle:-
:. perimeter formula = 2 x pi x r
shaded figure perimeter C= 1+2+3
1-> (2xpix(AB/2))/2
2-> (2xpix(BC+CD)2)/2
3-> (2xpix(AB+(BC/2))/2)/2
C= 2piAB+ 2piBC + 2piCD + 2piAB + piBC
"AB=BC=CD= a"
C= 2pia+ 2pia+ 2pia +2pia + pia
C= pi x a x 9
C=9pia = 9piAB = 9piBC = 9piCD
Regards.
8 May 2012 at 7:46 pm [Comment permalink]
The answer to the circle puzzle is 1.5 (pi) (r).
8 May 2012 at 8:50 pm [Comment permalink]
The perimeter of the shaded area is 2*pi*r
8 May 2012 at 11:10 pm [Comment permalink]
Let AB=BC=CD=X
Then 3X=2r
So X=2r/3
and r=3X/2
P(arcAD)=pi.r
P(arcAB)=pi.X/2
P(arcBD)=pi.X
P(fig)=pi(r+X/2+X)
P(fig) as a function of X---> pi(3X/2+X/2+X)= 3pi.X
P(fig) as a function of r---> pi(r+r/3+2r/3)= 2pi.r
The last one is very interesting.
P(fig) is the same as the perimeter of the circle with radius r.
8 May 2012 at 11:47 pm [Comment permalink]
New Puzzle
Line ABCD is a diameter of a circle whose radius is r. Length AB = BC = CD. Semicircles are drawn on AB and BD to create the shaded figure as shown.
What is the perimeter of the shaded figure?
Answer is 2*pi*r
9 May 2012 at 6:31 am [Comment permalink]
Solution to last puzzle: the three semicircles have radii r, r/2 and r/3, respectively. Their perimeters are r Pi, 2r Pi/3 and r Pi/3, respectively. The perimeter of the shaded figure is then the sum of the three perimeters above: 2 r Pi (the length of the larger circle circumference).
9 May 2012 at 5:54 pm [Comment permalink]
Puzzle solution is PI x D
12 May 2012 at 3:10 pm [Comment permalink]
Ans:?\pi r+pi 2r/3+pi r/3=2 pi r
23 Jul 2012 at 1:10 am [Comment permalink]
2*pi*r is the final answer
24 Jul 2012 at 5:16 pm [Comment permalink]
As radius=r therefore diameter=2r
Now Diameter of AB= 2r/3 and Diameter of BD= 4r/3
therefore, radius of AB= 2r/6 and radius of BD= 4r/6
Now
Perimeter of Semi Circle drawn on AB = (2*pi*r)/6
Perimeter of Semi Circle drawn on BD = (4*pi*r)/6
Perimeter of Semi Circle drawn on AD= pi*r
Perimeter of Shaded figure = (2*pi*r)/6 + (4*pi*r)/6 + pi*r =2*pi*r
6 Nov 2012 at 1:48 am [Comment permalink]
I think the answer is none other than 2 Pi r.
18 Dec 2012 at 10:06 am [Comment permalink]
Hi,
here is a business idea for you:
Make a math calendar for the coming years.
Each month can have a math puzzle or something.
I buy an astronomy calendar, and I would like to buy a math calendar.
If this is already done, please tell me where I can orden one.
Regards
Kofoss
18 Dec 2012 at 5:00 pm [Comment permalink]
@Kjell - Actually, this has been on my agenda for quite some time, but too late for this round! Hopefully there will be a 2014 IntMath Calendar.
Regards