IntMath Newsletter: Radius of curvature, easy math publishing with MathJax
By Murray Bourne, 18 Apr 2012
18 Apr 2012
In this Newsletter:
1. Radius of curvature interactive graph
2. Easy math input and nice output using ASCIIMathML and Mathjax
3. Math poll
4. Math puzzles
5. Final thought: Never stop
1. Radius of Curvature interactive graph
 |
Here's an interactive graph where you can explore the interesting concept of radius of curvature. This update now works in all browsers. I also added an explanation of where the radius of curvature formula comes from, under "Proof". |
2. Easy math input and nice output using ASCIIMathML and Mathjax
 |
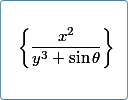Here's a system that allows for easy input of math (using calculator-like syntax) and good-looking output on any browser. Easy math input and nice output using ASCIIMathML and Mathjax Calling for volunteers: I need people to help with the conversion of images to MathJax. If you have some time, even if you can only do a few pages, it would be great to have your inputs. In the process, you'll learn this new system of math input, and learn some math notation. You'll also learn some math from doing it! Please let me know if you can help out, either via a reply to this email, or in the comments. |
3. Math polls
A poll during Mar/Apr 2012 asked readers: The math you are studying now - how useful is it for your future job?
It was gratifying to see more than half of those responding felt math is "very useful" for their future job. Many math educators believe we shouldn't worry about the "usefulness" of math, but I believe everyone - students and teachers alike - should know why we study various topics.
Sometimes the topic is included just because it's interesting (or gives some mathematical insight) which is fine, but when the topic has many "real-life" uses, everyone should know what they are. There are too many math students who struggle with the genuine question, "Why are we doing this?".
Very useful: 55%
Not useful: 19%
Somewhat useful: 14%
Don’t know yet: 13%
Total votes: 3400
Latest poll: The current poll asks readers about their use of math software. You can respond on any page in IntMath.com.
4. Math puzzles
There were plenty of responses to last Newsletter's puzzle on the coefficient of x99. Several people wrote correct answers (-5050), but gave no indication where their answer came from. It's always best to show your working! (Some people can just "see" the answer, but that doesn't help anyone else to know where it came from.)
Tom provided one of the more interesting correct answers, involving a "shift" to make things easier. This is often a good technique, to change the problem to one that is simpler.
Craig approached it using technology, and found his TI-89 calculator choked, but Mathematica software instantly gave him the answer.
Story: This math puzzle reminded me of the famous story where mathematician Carl Friedrich Gauss astounded his (terrible) teacher by adding the numbers 1 to 100 in just a few seconds. The teacher, a Mr. Buttner, was not a very nice person and would give his students very long calculations to do just so he could rest.
Gauss, aged 10 at the time, proceeded as follows. He paired the first and last numbers, then the inner 2 numbers and so on, like this:
1 + 100 = 101
2 + 99 = 101
3 + 98 = 101
He realized there would be 50 such pairs (1/2 of 100), so the total must be 101 × 50 = 5050.
Here are some other methods for finding this particular sum.
Latest puzzle: Find a 2-digit number equal to the square of the ten's digit plus the square of the sum of its digits
5. Final thought: Never stop
I've enjoyed helping others with math for as long as I can remember. And in the process of teaching others, I could see my own math skills improve.
Joseph Joubert, French Essayist and moralist (1754-1824), quite rightly said:
To teach is to learn twice. [Joseph Joubert]
The second and related thought is by an unknown writer:
Never stop striving, never stop learning, never stop teaching.
Your own math skills improve whenever you help others with their math difficulties. Don't do it for them - but help them to figure it out for themselves.
Until next time, enjoy whatever you learn.
See the 8 Comments below.
19 Apr 2012 at 12:01 am [Comment permalink]
Ten's digit=Y
Unit's digit=X
10Y + X = Y*2 +(Y+X)*2 (1)
Y and X must be Natural Numbers and Y = 0 and 5
X=1 ---> Y = 0 and 4
X=2 ---> Y = NOT A NATURAL NUMBER
X=3 ---> Y = COMPLEX NUMBER
Also for X=4;5;6;7;8;9 ---> Y = COMPLEX
If Y = 0 then no two-digit number.
So two solutions:
1. 50 test: 5*2 + (5+0)*2 =50
2. 41 test: 4*2 + (4+1)*2 =41
19 Apr 2012 at 12:05 am [Comment permalink]
Not sure where to respond to the latest puzzle but I suppose here will have to do.
After fiddling around for a bit I happened across 41 but couldn't provide a mathematical solution. At my university we use Matlab for a couple of subjects so I decided to write a program to do the guessing for me.
x = -1;
y = -1;
while x^2 + (x + y)^2 ~= 10*x + y
x = round(rand()*9 + 1);
y = round(rand()*9 + 1);
end
z = 10*x + y
And out popped 41. Most problems can be solved using this brute force method (with tweaks to the formula and random values)
19 Apr 2012 at 12:13 am [Comment permalink]
Some things disappeared and got mixed up while posting!
Y and X must be Natural Numbers and smaller then 10
Solving equation(1) for Y
2Y*2 + (2X-10)Y + X*2 + X =0
Y=-(2X-10)/4 +/- {(-4X*2 -32X + 100)*1/2 }/4
X=0 ---> Y=0 and 5
19 Apr 2012 at 3:05 pm [Comment permalink]
Puzzle:Find a 2-digit number equal to the square of the ten's digit plus the square of the sum of its digits:
Ans: 41
here we construct non linear equation and we solve the problem.
i.e Required number z= 10x+y
such that 10x+y=(x^2)+(x+y)^2
solving this equation we will get x=9/2 and y=-4
therefore z= 41
20 Apr 2012 at 6:55 pm [Comment permalink]
I am very happy with your work and just want to say thank you for your interest and time; I learn a gread deal from your work.
21 Apr 2012 at 1:17 am [Comment permalink]
this month's math puzzle. If I have read it right the answer should be 50.
the 5 in the ten's spot when squared = 25
the two digits that make the number 50 (5 + 0) when squared also = 25
25 + 25 = 50 the number I started with
25 Apr 2012 at 12:57 am [Comment permalink]
I AM CONVINCED THAT THE WORLD WOULD BE A BETTER PLACE WITH PERSONS LIKE YOU - WORKING WITH GENEROSITY AND WITH AN OPEN MIND ATTITUDE TO HELP OTHERS GROW.
THANK YOU VERY MUCH.
8 May 2012 at 11:11 pm [Comment permalink]
The solution for May 2012 puzzle:
AB=BC=CD=2r/3
But c=pi*r
Hence cAD=pi*r
cAB=pi*r/3
cBD=2*pi*r/3
cTOTAL=cAD+cAB+cBD=2*pi*r
Therefore; the circumference(c) of the shaded region is 2 pi r