IntMath Newsletter: Runge-Kutta, March math, Webinar
By Murray Bourne, 11 Mar 2015
11 Mar 2015
In this Newsletter:
1. Runge-Kutta Method
2. Special math days in March
3. Webinar: math on the Web
4. Math puzzles
5. Final thought - Sitting is killing us
1. Runge-Kutta Method for solving Differential Equations
 |
I recently updated the spring applet on this page: Work by a Variable Force using Integration The applet allows you to play with the spring, changing the spring constant (the "stiffness" of the spring) and seeing the resulting work done. |
"Work" in this context means the quantity arising from a constant force acting on a mass through a certain distance.
There is more work done when the spring is stiffer, and when you compress (or extend) the spring further.
In the javascript coding, I needed to use the Runge-Kutta Order 4 Method for obtaining the spring's position at a given time. This is a famous method for solving differential equations numerically. That is, we don't need to do any algebra to solve it - we use a numerical technique to find good approximations of the function values as time goes on.
I didn't have a section on Runge-Kutta in IntMath, so I wrote one. As an introduction, I wrote about Euler's Method, which is simpler than Runge-Kutta. Here are the new sections:
Euler's Method - a numerical solution for differential equations
Runge-Kutta RK4 numerical solution for differential equations
Numerical methods are very important in the field of computer solutions for calculus problems. In many cases, we can't solve the problem algebraically anyway, so we have to resort to numerical approaches.
Numerical methods are certainly worth knowing about as computer-based math becomes more the norm.
2. Special math days in March
(a) International Women's Day
International Women's Day was on 8th March. I wrote a story earlier about an interesting female math pioneer:
Another story is the astronomer who had to fight sexism to conduct scientific research: Vera Cooper Rubin. She was discouraged by her high school physics teacher, and couldn't enroll in Princeton for her masters because they didn't accept women in the program.
I think it's appalling that in many countries, women were not even allowed to enroll in universities until around a century ago. Sadly, in some countries that is still the case now. Malala Yousafzai is inspiring for the work she is doing to influence change in this area.
(b) Pi Day 2015

Pi T-shirt [Image source: themetapicture]
There is usually a flurry of activity regarding "pi" on 14th March each year, since the first 3 digits of the decimal approximation for pi are 3.14.
This year is a bit more special, as the next 2 digits of pi are 15, so we have 3.1415, or 3/14/15 (as written in the USA).
Happy Pi Day!
3. Webinar: Mathematics on the Web
An IntMath reader recently asked if I could conduct a Webinar on how to write mathematics on the Web.
There are many times when students want to ask their teachers a math question via email, and resort to writing it on paper, then photographing it and attaching it to the mail. This is not the best way.
Similarly, in math help forums, it's difficult for those asking questions and those answering them to easily communicate math symbols, fractions, formulas and the like.
For math teachers it is troublesome to create lessons on the Web for the same reasons.
So I'm considering offering a Webinar on ways to solve these issues. It will include:
- How to easily write math on a Web page
- How to set up a forum so students can communicate math concepts easily
- Communicating math via email
If you would like to be part of this one-hour Webinar (date and time to be decided), let me know by responding to this mail, or here.
There'll be a nominal fee for the session.
4. Math puzzles
The puzzle in the last IntMath Newsletter asked about the value of n which gives a maximum in a certain sequence.
The correct answer with explanation was given by Tomas, Thomas, Dineth, Nicos, Hamid, Michael, Henry, Francis, Helena, and Francisco.
It was interesting to see the variety of approaches used - they were almost all unique.
Here's another way to attack that question - draw a graph! We can see there's a local minimum at the point (6,523) and so the integer just before this is n = 5.
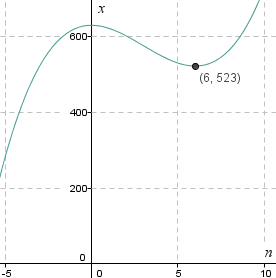
Of course, we would need to do some algebra (or calculus, or trial-and-error) to prove n = 6 is actually the local minimum and not a point which is "close by". (Arguably my graph shouldn't be a curve. Can you say why?)
New math puzzle: To celebrate Pi Day, here's an interesting conundrum I came across recently. It involves limiting processes, a key concept in mathematics.
This claims Pi = 4. How can it be so?
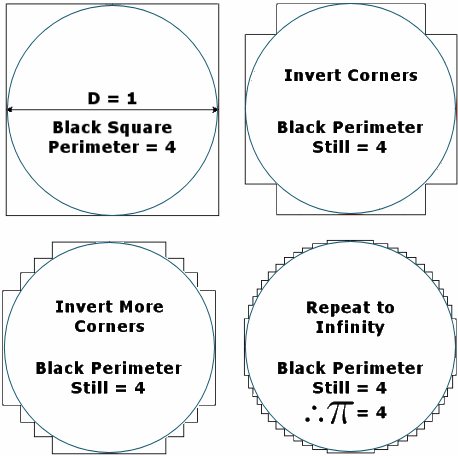
Leave your responses here.
4. Final thought - Sitting is killing us
For the last 20 years, I've spent the majority of each day sitting in front of a computer (or tablet, or smart phone). My body is not happy with me, and it objects by giving me clear messages - like a sore back, numb legs, painful arms and RSI-affected fingers.
So reently I've been trying to move (or at least stand) more during each day. I now consume information (watching videos, reading articles, and clearing emails - where I don't need to use a keyboard) while standing as much as possible. It's helping, but not as much as I'd like.
Many of you will be involved in sedentary work now or in the future. Do yourself a favor and move around more. I wish I'd done so.
 |
In this animation from TED, we learn why we shouldn't spend our lives sitting. |
Until next time, enjoy whatever you learn.
See the 6 Comments below.
11 Mar 2015 at 11:36 pm [Comment permalink]
The limit will give the area of circle but the lengths do not depict the correct limit. For the circle the elemental lengths have to be perpendicular to radius. In the square the lengths are in different orientation and so it can not give the circumference in the limit.
12 Mar 2015 at 12:34 am [Comment permalink]
Murray, I like your newsletter very much. You are helping me to amaze all the people who think I am a dunce...especially my brother the engineer 🙂
13 Mar 2015 at 6:39 am [Comment permalink]
this month looks exciting, I have to wait a few days
to get into it, am working on my car at this time.
but I did review it.
13 Mar 2015 at 6:04 pm [Comment permalink]
I have enjoyed reading this article! kudos!
16 Mar 2015 at 1:13 am [Comment permalink]
All the lines are either horizontal or vertical.
Examine the horizontal lines at the top half
of ANY of the figures
and it will be seen that they can be joined
together to make-up the diameter D = 1.
Similarly so for the lower half, the horizontal
bits add to D=1
Likewise the left side and right side vertical lines
each add to D = 1
So in EACH figure the total line length = 4D,
As the steps become smaller we are MISLED into
thinking the line length = the circle circumference,
Which is that 4D = circumference.
Instead pi x D being = the circumference.
Lateral thinking.
Happy St.Patrick's Day to all. Taking the
three leaf shamrock and it's simple 3 as the
circumference to diameter ratio, it's only 5% short!
Also, many electrical and electronic circuits
work very well with components having +/- 10% tolerance! So perhaps taking 4 as the ratio may be
satisfactory for the digital age considering that
as 4 it's a handy 2^2.
Mad? What does a bird know about aeronautics?
24 Mar 2015 at 4:12 am [Comment permalink]
On your first question: "Arguably my graph shouldn’t be a curve. Can you say why?" The puzzle was concerned with integral values, and the rest were undefined. Yet, some of us -including myself- used a continuous curve as a device for solving the problem using derivatives. I think it suffices to make this explicit.
The new puzzle: Each "inversion" of corners results in a new graph, but the perimeter remains constant, i.e., it is a sequence of constant values whose the limit is 4. The graph appears to converge to the perimeter of the circle, but it is just an optical illusion. It is actually a highly spiked polygon. Contrary to other methods, like Archimedes' approximation, where successive values are a decreasing - or increasing - sequence converging to Pi.