IntMath Newsletter: Model, animations, software
By Murray Bourne, 29 Aug 2018
29 Aug 2018
1. New on IntMath
(a) EFFEKT bridge model
 |
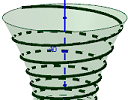In the last Newsletter, the puzzle was to model the EFFEKT bridge, a spiral in the shape of a hyperboloid. Here's my solution: |
(b) Math Art in Code: Animated Lissajous figures
 |
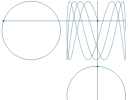We can get interesting and beautiful curves when combining two signals. See: |
2. Resources
(a) oPhysics interactive simulations
 |
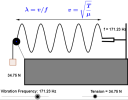Here's over 100 physics simulations including kinematics, forces, waves, fluids. There's even circuit drawing tools. |
(b) Topology and Geometry Software
In the article, With new technology, mathematicians turn numbers into art, we read how various mathematicians are pushing the envelope when it comes to exploring mathematical concepts within the real and virtual realms.
[Image source: Frank Farris, CC BY]
One of the resources mentioned in that article is the following, developed by Jeff Weeks, one of the "rock stars" of the mathematical world.
 |
In these games with a mathematical underpinning, you can explore polyhedra (tetrahedrons, icosidodecahedrons, etc) and 4-D mazes. You can even play pool on a hyperbolic surface. Some are for mobile devices, others for desktop. Go to: |
The development of these games was supported by the (US) National Science Foundation.
3. Math in the news
What is the smallest number of colors that you'd need to color any graph consisting of points connected by segments of the same length?
This puzzle has fascinated mathematicians since the 1950s when it was first posed. It was long held that 4 colors should do the job.
 |
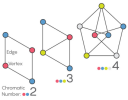However, earlier this year, amateur mathematician Aubrey de Grey proposed the first unit-distance graph that requires at least five colors. Here's the article: Decades-Old Graph Problem Yields to Amateur Mathematician |
4. Math Movies
(a) 3 Ways to spot a bad statistic
 |
We're living in a world of "alternative facts", but this is a dangerous situation. It's crucial we understand how statistics are collected, funded, interpreted and used. |
(b) How does your body know what time it is?
 |
The story of Michel Siffre is a fascinating one. He went into a cave for months to see the effect on his perception of time. |
5. Math puzzles
The puzzle in the last IntMath Newsletter was about the EFFEKT bridge, which I addressed earlier in this Newsletter.
New math puzzle: Factorial
What's the maximum number of times 2 can divide exactly into factorial 50 (written 50!)?
You can leave your response here.
6. Final thought
"Learning is not compulsory - neither is survival."
[W. Edwards Derning]
Until next time, enjoy whatever you learn.
See the 11 Comments below.
29 Aug 2018 at 4:31 pm [Comment permalink]
I am interested in determining the velocity of Time; i.e., At what speed does time elapse between second 1 and second 2.
At the moment I am stuck with the proposition that times moves at the rate of 15 degrees per hour.
Can you point in the right direction?
Siggy
29 Aug 2018 at 5:49 pm [Comment permalink]
@Siggy: Well, I'm not sure that you can find the velocity of time, or whether that quantity actually has any meaning.
However, you could find the angular velocity of an analogue clock's hand as it rotates. So for the hour hand, the rotation in one second would be:
15° / 3600 = 0.00416666°
So the (angular) velocity of the hour hand is 0.00416666° / sec.
29 Aug 2018 at 6:01 pm [Comment permalink]
The maximum power of 2 in 50! will be
[50/2]+[50/2^2]+...+[50/2^5]= 47
30 Aug 2018 at 12:06 am [Comment permalink]
50! is a product of 50 numbers from 1 to 50. Among these 50 numbers, there are 25 even numbers that can each be divided evenly by 2; there are 12 that are multiples of 4 that can evenly be divided by 2 again; there are are 6 that are multiples of 8 that can be evenly divided by 2 again; there are 3 that are multiples of 16 that can be evenly divided by 2 again; and there is one number that is a multiple of 32 that can be divided by 2 again.
25+12+6+3+1 = 47
In 50!, 2 is a factor 47 times, so 50! can be evenly divided by 2 up to 47 times.
30 Aug 2018 at 5:15 am [Comment permalink]
In the integers from 1 to 50,
there are 25 numbers divisible by 2
There are 12 that are divisible by 4
There are 6 that are divisible by 8
There are 3 that are divisible by 16
There is 1 that is divisible by 32
25 + 12 + 6 + 3 + 1 = 47 powers of 2
31 Aug 2018 at 12:12 pm [Comment permalink]
The Answer is 214 times.
Because:-
50! > = 2^ n
So n root(50!) > = 2
215root(50!) = 1.994 . . . Too low, but try adjacent integer root.
214root(50!) = 2.001 . . . Just there, with some remainder
So 2 can be divided into 50! 214 times, with a < 2 remainder.
In 80th year, still unable to do HTML, sorry.
31 Aug 2018 at 12:58 pm [Comment permalink]
Proof was shown in previous reply, but calculation was omitted in error.
Calculation,
Log base2 50! = 214.2. So 214 = Answer as shown before.
1 Sep 2018 at 7:17 am [Comment permalink]
I Have learned a lot, computer software is amazing.
ThankX for teaching all that stuff
6 Sep 2018 at 4:26 am [Comment permalink]
Obviously the odd integers do not have 2 as a factor.
Then the integers 2, 6, 10, 14, 18, ... ,50 each have only one factor of 2. Then 13 in all.
The integers 4, 12, 20, 28, 36, 44 each have two 2s . Then 12 2s in all.
The integsrs 8, 24, 40 have three 2s. Then 9 2s in all.
The integers 16 and 48 have four 2s. Then 8 2s in all.
The last integer, 32, has five 2s. Then 5 2s in all.
Now add 13 + 12 + 9 + 8 + 5 = 47.
Answer is 47.
i.e. 2^47 will divide into 50!.
25 Sep 2018 at 5:04 pm [Comment permalink]
I initially started working with
but then I remembered bodmas.
In the end I realised I don't know anything about maths and just got excel to tell me: 167 times
2 Oct 2018 at 5:31 pm [Comment permalink]
Thanks very much intMath.
This is awesome.This has really made me understand alot of funny mathematics here. Thank you ?.