IntMath Newsletter: Inverse animations, finding quintic functions
By Murray Bourne, 29 Mar 2016
28 Mar 2016
In this Newsletter:
1. Inverse trigonometric graph animations
2. How do you find the function for a given quintic curve?
3. Math in the news
4. Math puzzles
5. Math movies: 3Blue1Brown
6. Final thought: Keep trying
1. Inverse trigonometric graph animations
| These animations demonstrate how the inverse of a function is a reflection in the line y = x. |
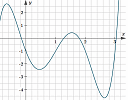
2. How do you find the function for a given quintic curve?
|
A quintic curve is a polynomial of degree 5. Given such a curve, how do you work backwards to find the original function expression? How to find the equation of a quintic polynomial from its graph |
3. Math in the news
a. Bitcoin transaction delays
Earlier this month, the cryptocurrency Bitcoin network "reached its capacity, causing transactions around the world to be massively delayed, and in some cases to fail completely", according to Bitcoin transaction delays: Is block size increase the final answer?
A bitcoin is a 256 bit binary number that has met certain "conditions". The "conditions" only allow for some 21 million coins, and some 13 million coins have so far been discovered i.e. "mined". The value of bitcoins has varied between less than $1 up to $1000 between 2011 (when it was first released) to now, when it is around $415.
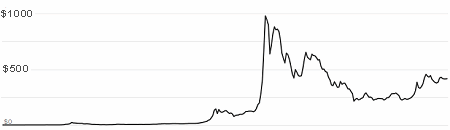
Value of Bitcoins since launch
Bitcoins are organized via the Block Chain, a distributed database on thousands of computers, that records the birth and every transaction of every coin.
The problems with transaction time result from the system only being able to process about 7 transactions per second. With a backlog of some 20,000 transactions on March 3rd, people were waiting in stores for over 30 minutes. There has been a lot of discussion about how to fix the technical problems, including increasing the memory allocation.
Bitcoins, or something like them, are part of our future, since they offer a way to reduce the stranglehold of the big banks. See other potential uses for bitcoins in "15 More Amazing Ways Bitcoin Changes the Future of Money".
b. With Math I Can
|
|
Too many people see mathematics as just a set of formulas, algorithms and calculations. Sadly, they miss what it's really all for, end up with negative views and feel they will never "get" it. Amazon was encouraging a math "growth mindset" through its With Math I Can strategy, but it has since disappeared. |
Growth mindset is based on Stanford University-based Jo Boaler's research on inquiry based learning, gender equity and math anxiety.
On the site, we read that Boaler's colleague Carol Dweck found that...
... students who believed that their ability and intelligence could grow and change (otherwise known as growth mindset) outperformed those who thought that their ability and intelligence were fixed.
I believe addressing student emotions and attitudes toward math is one of the keys to success. However, Boaler's work has not been without controversy (see Your Brain on Maths: Educational Neurononsense Revisited).
c. Shape derivatives to achieve 27% cost efficiencies
|
|
Ever heard of shape derivatives? In their work to improve electric motor efficiency, researchers at Johannes Kepler University used shape derivatives to optimize the cost functional. See: |
The published paper:
Shape optimization of an electric motor subject to nonlinear magnetostatics [PDF]
[Hat tip to Pi Po for alerting me to these stories.]
4. Math puzzles
The puzzle in the last IntMath Newsletter asked about the maximum value for a particular fraction involving 3 distinct integers.
Correct answers with the most convincing (and elegant) explanations (those which adequately explained why) were given by: Don, Tomas and Ben. There were plenty of correct answer submissions, but not all adequately investigated all the possibilities.
A lot of the time we can "see" the answer to a mathematical problem, but we need to explain it to others (who don't have such insights) in such a way that we cover all the possibilities.
New math puzzle
Two girls need to go to the next town, 40 km away, as quickly as possible, and they have one bicycle between them. Peta walks at 4 km/h and Noni walks at 8 km/h, while both cycle at 16 km/h. Only one girl can ride the bicycle at one time.
What is the shortest time they can take to reach the next town?
You can leave your responses here.
5. Math movies: 3Blue1Brown
|
Grant Sanderson has produced some great math videos at 3Blue1Brown. You'll find videos on Fractals, Music, Binary Counting and Calculus. They are well-expressed and thought-provoking. See: 3Blue1Brown |
6. Final thought: Keep trying
On the WithMathICan site, there's a great quote from Thomas Edison:
"Our greatest weakness lies in giving up. The most certain way to succeed is always to try just one more time."
Until next time, enjoy whatever you learn.
See the 13 Comments below.




29 Mar 2016 at 7:38 pm [Comment permalink]
Dear Mr. Bourne,
I appreciate your monthly letter and although I only teach up to the Algebra 1 level, I always find something useful for my own edification if not that of my students. I read with particular interest your comment and especially the link for additional comments on the growth mindset "phenomenon" that has the world of education in a tizzy. I have been searching for a scholarly critique of the ideas expressed by those at the forefront of the craze. After reading down through the comments to the author of the post I think I see why there hasn't been much posted to address the claims of the movement. They appear to be a bit sensitive to critique and quick to engage with litigation instead of truth. I bought the Mathematical Mindset book that claims that thousands of math teachers have seen the light and will be turning the world upside down with the secrets to learning contained within. I began reading with a similar hope and then came to this quote, If we do "test and grade, [students should be given] the same grade, or higher, for mistakes, with a message attached that the mistake is a perfect opportunity for learning and brain growth" and it took me two months to pick the book up again. It appears that the education world is so hungry for a quick fix that it will latch onto just about anything. As part of my search for sense in the midst of this "crystals and incense" age, I was referred to the document at this link http://dx.doi.org/10.1037/rev0000025 which helped me put it in perspective. We clamor for some new way to do something I think most of us know inside of us. Learning requires effort and effort demands perseverance. It seems the framers of the Common Core standards in the US knew this when they made the first of eight pillars of the learning of math "Make sense of problems and persevere in solving them." After 59 years of living on this earth I firmly believe that there are no quick fixes to learning. There may be more effective ways to teach some content but when the learning to be done is not simplistic, it takes effort and the desire to keep at it until one has finally achieved it. Thanks for your efforts in helping us understand and giving us reasons to stick to it.
Sincerely,
Glenn McIntyre
Teacher of Mathematics
Hoping not to be referred to anyone's attorney's in the event I have disagree too vigorously.
29 Mar 2016 at 7:58 pm [Comment permalink]
@Glenn: Thanks for your passionate response. Yes, this issue does press buttons!
The Bowers paper (at least the extract) seems to be professional sour grapes to me. I don't know that "Evidence that the brain changed in response to instruction is irrelevant." We are in the business of changing brains, surely? But I do agree with him that observable behaviors should be given more prominence - not only in research but in education generally.
30 Mar 2016 at 2:39 am [Comment permalink]
Hi Murray: You put in Math News, Bitcoin notice?
Best Regards.
30 Mar 2016 at 4:52 am [Comment permalink]
@luis: Yes, a Bitcoin is really a mathematical construct.
30 Mar 2016 at 5:56 am [Comment permalink]
As far as I can tell, the optimum method would be for the slow walker to cycle for a while, then leave the bike and walk the rest of the distance. The fast walker starts walking and picks up the bike after the distance and they arrive at the same time.
total time = distance1/bikeSpeed + distance2/slowWalkingSpeed
total time = distance1/fastWalkingSpeed + distance2/bikeSpeed
distance2 = 40 - distance1
Set those two equations equal and we have just one unknown, distance1, which turns out to be 30 km. Substituting this back into one of the equations gives us the total time of 4.375 h
This is good because we know it must be less than if the fast walker just walked the whole way (5 hours)
4 hours 22 mins and 30 seconds
30 Mar 2016 at 6:09 am [Comment permalink]
Minimum time is when the slowest walker walks a minimum distance, which is zero. This
Minimum time is 40/8=5hrs
30 Mar 2016 at 6:33 am [Comment permalink]
First Peta takes the bicycle for (t1)h and then walks for (t2)h.
The Noni to arrive to get the bike wants [2*(t1)]h (8=16/2) and after moving to
[(t1)-(t2)]h. They arrive simultaneously.
16(t1)+4(t2)=40 (1)
8*2(t1)+16[(t1-t2)]=40 (2)
(1), (2): (t1)=(12,5/6)h=125min, (t2)=(10/6)h=100min, (t1)+(t2)=(22,5/6)h=225min
30 Mar 2016 at 11:22 pm [Comment permalink]
Shortest journey time is 5 hours.
Because;
Noni can walk the whole 40km @ 8 Km/h in 5 hours.
If Peta was to walk any part of journey @ 4 Km/h
any shared walking journey time would take longer than 5 hours.
So Peta cycles the whole journey of 40 Km @
16 Km/h in 40/16= 2.5 hours.
So shortest time for BOTH to get to next town is 5 hours.
No math equations, just a bit of observation and logic!
31 Mar 2016 at 9:13 am [Comment permalink]
Each of the two girls uses the bicycle for a proportion of the length of the travel, so that the two proportions add up to 1. Suppose that Peta uses the bicycle for a proportion p of the distance to the next town, so that Noni will use it for a proportion 1 - p. Then the average speed Peta will travel is 16 p +4 (1 - p), while the average speed of Noni's is 8 p + 16 (1 - p), both in km/h.
The time needed to travel 40 km is equal to 40 divided by the average speed, so it will be 40/((16p+4(1-p)) for the first girl, and 40/((8p+16(1-p)) for the second girl. The first one is decreasing with p, while the second one is increasing. The shortest time for both to reach their destination is equal to the maximum of the two times of arrival. This implies that the shortest time altogether corresponds to that value of p for which both times of arrival are equal.
The point of intersection of the two functions of p is p = 0.6, which makes the shortest possible time equal to 3.57 hours, i.e., 3 hours and 34 minutes. The girls will have to share the bicycle in such a way that Peta uses it 60% of the distance, i.e. 24 km, and Noni for 16 km, in whatever way they wish.
4 Apr 2016 at 6:10 pm [Comment permalink]
the shortest time is 1hr 30 min.PETA CYCLES 1 HR AND WALKS 30 IN ,NONI WALKS 1 HRS AN CYCLES 30 MIN
6 Apr 2016 at 3:06 am [Comment permalink]
P=peti, n=Nani, w=walk,b=bicycle.
Tpeti=xpw/4+xpb/16, tnani=xnw/8+xnb/16,
Xpw =xnb,xpb=xnw,xnb+xnw=40,tpeti=tnani,
xnw=30,xnb=10
T=35/8 hr or 262.5 min.
9 Apr 2016 at 9:55 pm [Comment permalink]
Time =Distance/speed
t = 40/8 = 5hours for Noni
t = 40/4 = 10hours for peta
and t = 40/16 = 2.5 hours for riding
The shortest time is when Noni walks and Peta rides and it will take 5 hours for both to be in the next town.
27 Apr 2016 at 11:25 am [Comment permalink]
the shortest time for two girls go to near town is 35/8