Functions
By Murray Bourne, 22 Feb 2010
A lot of people have difficulty with functions in math. I suspect it's because function notation is not very learner-friendly.
Yousuf, one of my regular correspondents, got stuck on the following problem recently.
What is the area of the rectangle ADEB shown in the diagram?
The curve is the graph of y = 1/x2 (for positive x), and r is some arbitrary value of x.
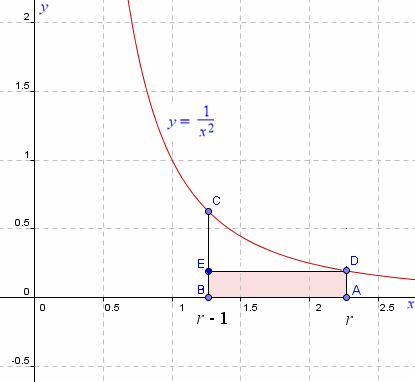
We'll come back to this question a little later. I suspect his problem with this question was due to a rusty conceptual understanding of functions.
Functions Overview
A function is simply an expression involving variable(s).
We usually write a function of the variable x using the notation: f(x). A function has at most 1 value for each value of x.
For example, if f(x) = 5x2 + 3, we can find the value of the function if we choose x = 0 as follows.
f(0) = 5(0)2 + 3 = 5 × 0 + 3 = 3
Now, this is a good example of the notation problem I was talking about at the beginning. We write "f(0)" (f bracket 0 bracket) to mean "evaluate the function expression by substuting 0 every time we see an x" and we see this on the left hand side of this equation.
But on the right hand side, I have written "5(0)2" (5 bracket 0 bracket squared) and this means "5 × 02". We need to be careful with this - writing 2 different concepts with what is essentially the same notation.
It is a shame that function notation is so clumsy and causes problems for newbies.
Let's look at some more examples for our function f(x) = 5x2 + 3.
f(2) = 5(2)2 + 3 = 5 × 4 + 3 = 23.
f(10) = 5(10)2 + 3 = 5 × 100 + 3 = 503.
If we were to substitute many more values of x and plot the dots on a graph, we would get the following:
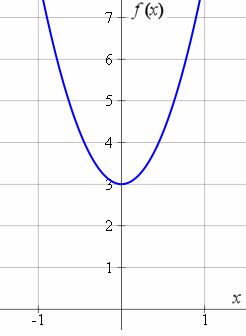
Note: On the vertical axis, I put f(x), but I could have also put "y", since the convention in math is the vertical axis represents the function value. Often you'll see it written y = f(x).
OK so far?
Now, let's make things a bit more interesting. What is f(a)? We just substitute a everywhere there is an x in the original function, like we did before with the numbers:
f(a) = 5(a)2 + 3 = 5a2 + 3
Let's do another. In this next case, f(a + 4), we are just replacing each x in the original function expression with a + 4.
f(a + 4) = 5(a + 4)2 + 3 = 5(a2 + 8a + 16) + 3 = 5a2 + 40a + 83
Of course, we need to be careful to expand out the brackets properly!
A Different Function
Let's change our function to 
.
This is the curve we met in the question at the the beginning of this article.
If x = 1, we replace every x in our expression with 1 and we have:
What f(1) means on a graph is the distance from the x-axis to the graph is 1 unit. The function value is the height of the graph for that x-value.
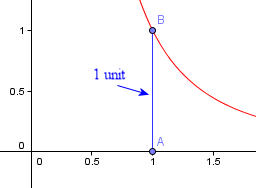
Now let's do f(3a).
The value
represents the height of the graph when x = 3a. We need to be careful with the brackets.
Back to Our Problem
Here's the graph again:
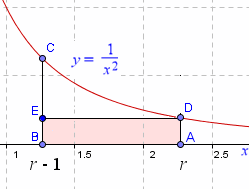
So how do we find the area of the rectangle BADE? The width of the rectangle is quite straightforward, as the distance from r to r − 1 is just 1 unit. But we need to find the height AD.
AD is just the function value f(r):
So the area of the rectangle is just
Area = width × height = 
What if we needed the height BC?
We would just find the function value as follows.
BC = 
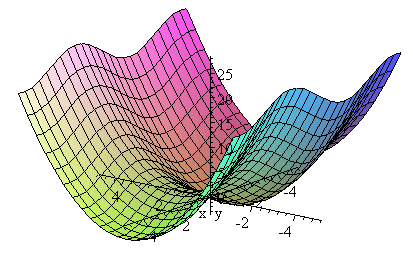
Functions of 2 Variables
The functions above only have one variable and they describe a curve in 2-D space.
To describe a 3-D surface, we need to use 2 variables.
We write a function of 2 variables using this notation:
z = f(x,y)
The "z" indicates the height of the surface for particular values of x and y.
An example of a 3-dimensional surface is z = x2 + 3 sin y.
More Information
See this chapter for a lot more examples of functions: Functions and Graphs. (2 dimensional)
This is an introduction to 3-dimensional Coordinate System.
See also Towards more meaningful math notation where I suggest an alternative to the current confusion.
See the 14 Comments below.
26 Feb 2010 at 2:24 am [Comment permalink]
I am just an old retired engineer that wants to catch up on things once in a while or solve a math problem that I have forgotten how to solve.
The above was interesting but I assume that the f(10) you show above has a typo.
f(10) = 5(10)2 + 3 = 5 × 100 + 3 = 103
It should be:
f(10) = 5(10)2 + 3 = 5 × 100 + 3 = 503
Right?
26 Feb 2010 at 2:28 am [Comment permalink]
Functions is the difficult part to most of the students who are doing basics in univesities. more examples is required. thanks for this topic
26 Feb 2010 at 9:08 am [Comment permalink]
Thanks Jim. I've fixed the typo.
27 Feb 2010 at 2:43 pm [Comment permalink]
Quiet helpful. I expect more examples.
Thank you very much.
28 Feb 2010 at 3:30 pm [Comment permalink]
Thanks as always. Your topics are all very interesting.
28 Feb 2010 at 7:48 pm [Comment permalink]
Your news letters are very refreshing
ahmed
1 Mar 2010 at 10:50 pm [Comment permalink]
Your explanations are quite understanding. I am impressed you explain the topic even with examples before you go on to answer the question posed by a reader. Give us more of those!!
2 Mar 2010 at 11:28 am [Comment permalink]
Very good. what is the area of ABCD?
4 Mar 2010 at 10:28 am [Comment permalink]
Hi Ted
Area ABCD requires finding the area under a curve, and this involves Integration.
This is how it works for this particular example.
Area ABCD =
Once you know the value of r you can find the area. So for example, if r = 4,
4 Mar 2010 at 10:35 am [Comment permalink]
I liked your explanation of the solution as it provided simple examples and presented them logically, one piece at a time. I teach math and also have a Masters in Applied Financial Math, so I have no problem with the subject; however, I find many high school students struggle mightily with it.
I’m going on a tangent here for a bit with a sad story. A few months ago I visited a 9th grade public school classroom where the teacher had an incorrect understanding of functions! She had posted some “exceptional work” from a student which said, “In a function, for every y-value there is only one x-value.”
Well, that was news to me as clearly the opposite is true for a function: for every x-value (or input) there is only one y-value (or output). Ironically, the example graphed was the function f(x) = y = 5, where for one y-value there are an infinite number of x-values as every x results in a y of 5!
This teacher went on to write that the “vertical line test” (which is a correct test for a function) proves that it is a function. The vertical line test says that any vertical line (a line composed of all the points that share the same x-value) can only cross a function at one point; this is simply another way of saying that for any x-value there can be only one y-value.
Worse was that she was teaching this backward definition to her students and had them copying it in their “Math Dictionaries” during class. Fool that I am, I felt the need to tell her about the error after class, so she could correct it for the students. The response shocked me. She steadfastly claimed that her definition was correct and was in the textbook. I wrote a detailed explanation an included the functions f(x) = y = 5 and f(x) = y = x2, both examples she had posted on the wall. I pointed out that if y = x2, when x = -2 then y = 4 and when x = 2 then y = 4 also!
Unfortunately, either she could not understand the concept or refused to acknowledge making a mistake. She stuck with her opinion even after I left her the definition copied from the back of her textbook which used the terms input and output. I guess that was why I was asked to observe/help in her classes. In summary, I feel that it is tragic that situations like this exist in our educational system.
4 Mar 2010 at 10:38 am [Comment permalink]
Thanks for the story, Damon.
Some math teachers use one textbook only, and therefore miss vital concepts.
It's interesting how she was strongly opposed to a different POV.
5 Mar 2010 at 1:42 am [Comment permalink]
This piece makes interesting reading.It is a piece from a classfoom teacher and not just passerby in teaching profession.As a math teacher myself , I enjoy the piece. WELL DONE!
3 Apr 2010 at 5:10 pm [Comment permalink]
i actually didnt understand functions bt nw at least im having something to present in class
3 Oct 2010 at 12:49 am [Comment permalink]
SIR,
Nice work.Most useful for all ages,students or parents.
Thanks.