How to reflect a graph through the x-axis, y-axis or Origin?

This mail came in from reader Stuart recently:

Can you explain the principles of a graph involving y = −f(x) being a reflection of the graph y = f(x) in the x-axis and the graph of y = f(−x) a reflection of the graph y = f(x) in the y-axis?

Thanks

My reply

Hello Stuart

Let's see what this means via an example.

Let f(x) = 3x + 2

If you are not sure what it looks like, you can graph it using this graphing facility.

You'll see it is a straight line, slope 3 (which is positive, i.e. going uphill as we go left to right) and y-intercept 2.

Now let's consider −f(x).

This gives us

−f(x) = −3x − 2

Our new line has negative slope (it goes down as you scan from left to right) and goes through −2 on the y-axis.

When you graph the 2 lines on the same axes, it looks like this:

Note that if you reflect the blue graph (y = 3x + 2) in the x-axis, you get the green graph (y = −3x − 2) (as shown by the red arrows).

What we've done is to take every y-value and turn them upside down (this is the effect of the minus out the front).

Now for f(−x)

Similarly, let's do f(−x).

Since f(x) = 3x + 2, then

f(−x) = −3x + 2 (replace every "x" with a "−x").

Now, graphing those on the same axes, we have:

Note that the effect of the "minus" in f(−x) is to reflect the blue original line (y = 3x + 2) in the y-axis, and we get the green line, which is (y = −3x + 2). The green line also goes through 2 on the y-axis.

Further Example

Here's an example using a cubic graph.

Blue graph: f(x) = x³ − 3x² + x − 2

Reflection in x-axis (green): −f(x) = −x³ + 3x² − x + 2

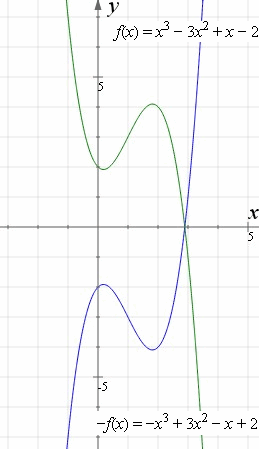
Now to reflect in the y-axis.

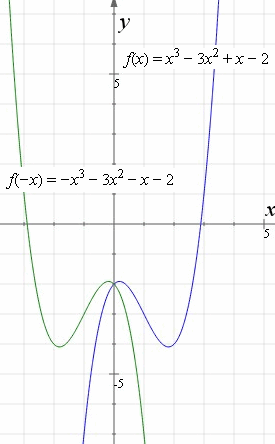
Blue graph: f(x) = x³ − 3x² + x − 2

Reflection in y-axis (green): f(−x) = −x³ − 3x² − x − 2

Even and Odd Functions

We really should mention even and odd functions before leaving this topic.

For each of my examples above, the reflections in either the x- or y-axis produced a graph that was different. But sometimes, the reflection is the same as the original graph. We say the reflection "maps on to" the original.

Even Functions

An even function has the property f(−x) = f(x). That is, if we reflect an even function in the y-axis, it will look exactly like the original.

An example of an even function is f(x) = x⁴ − 29x² + 100

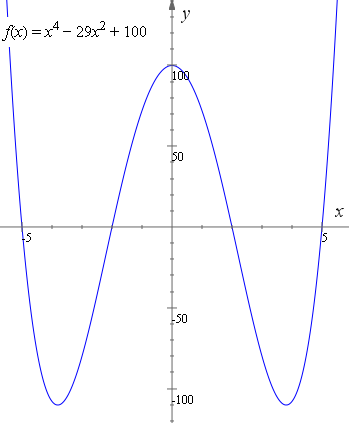
The above even function is equivalent to:

f(x) = (x + 5)(x + 2)(x − 2)(x − 5)

Note if we reflect the graph in the y-axis, we get the same graph (or we could say it "maps onto" itself).

Odd Functions

An odd function has the property f(−x) = −f(x).

This time, if we reflect our function in both the x-axis and y-axis, and if it looks exactly like the original, then we have an odd function.

This kind of symmetry is called origin symmetry. An odd function either passes through the origin (0, 0) or is reflected through the origin.

An example of an odd function is f(x) = x³ − 9x

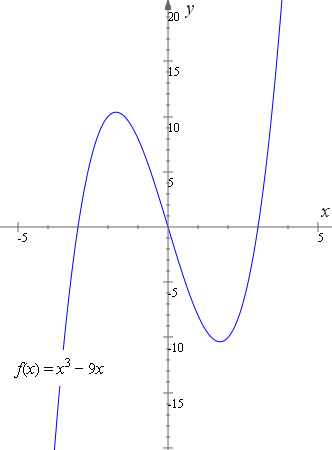
The above odd function is equivalent to:

f(x) = x(x + 3)(x − 3)

Note if we reflect the graph in the x-axis, then the y-axis, we get the same graph.

More examples of Even and Odd functions

There some more examples on this page: Even and Odd Functions

Knowing about even and odd functions is very helpful when studying Fourier Series.

I hope that all makes sense, Stuart.

 

 

See the 8 Comments below.