Partial differentiation - what is it about?
By Murray Bourne, 20 Jan 2009
Barbara, a reader from Mauritius, wrote recently:
What is the significance/logic behind partial derivatives? Why do we use it? I know it’s for functions involving 2 or more variables but the logic is not clear to me.
Multi-dimensional math is often hard to get your head around on the first hearing. The section on partial derivatives comes at the end of the introduction to the concept of derivatives. It would help if students have learned about 3-D geometry first.
Back to Barbara's mail. Here is my reply.
Hello Barbara
You could think of it like this. Say we are doing a car journey and we have no air conditioner in the car (so we notice the temperature).
The temperature in the car will depend on several things, but let’s restrict it to 3:
* How far north or south we are
* How high we are (altitude)
* The time of dayLet's now go from the tip of South America to the northern reaches of Canada, non-stop. We'll be going from the southern hemisphere across the equator to the northern hemisphere, up and down mountains, daytime and night-time.
So the temperature T will be a function of distance (x) from the equator, altitude (h) and time (t). In math-speak, we write this as:
T = f(x, h, t)
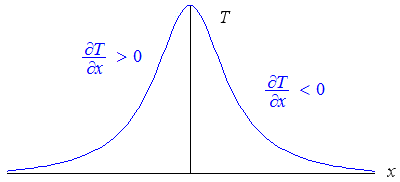
Now let’s consider partial dT/dx, which we write as ∂T/∂x. For this, we ignore height and time. The temperature will be low when we start (near the South Pole), get hot in the middle (as we pass the equator) and get cold again when we get to Canada. The graph of T against x will be bell-shaped and ∂T/∂x will be positive for the first half and negative for the second, something like the following.
Next, consider partial ∂T/∂h. This time, we ignore x and t. Now the value of T will be higher on the coast than in the mountains, and will be up and down for the whole journey. Partial dT/Dh will vary between positive and negative throughout the journey.
Finally, ∂T/∂t. Keeping x and h constant, the temperature will be low in the mornings, higher in the middle of the day and then low again in the evenings. Partial dT/dt will be positive from dawn to around mid-day each day and negative for the rest of each day, something like our bell-shaped curve above.
So the idea of partials is to strip away all the other variables and just concentrate on one pair of variables at a time (the dependent variable and one of the independent variables). This is very important in any science experiment, as we need to test each variable to see what effect it is having on the overall picture.
Hope that helps.
Barbara replied:
hi
Thanks for the mail. Really helpfull!!! Now i have a broader picture of how it works.
You’re welcome, Barbara.
See the 19 Comments below.
25 Mar 2009 at 11:25 pm [Comment permalink]
When we do partial differentiation instead of normal differtionion?
28 Mar 2009 at 8:17 pm [Comment permalink]
Hi Shaikh
If you only have one independent variable, then you need to do ordinary differentiation.
Partial differentiation is needed if you have more than one independent variable. In the story above, there are 3 independent variables, distance (x), height (h) and time (t), so I used partial differentiation.
26 Feb 2010 at 4:02 am [Comment permalink]
an excellent site... i am a secondery math teacher.. i really found a great benefit reading.. and reading the given information.. I am so happy to join this site..
Thank you so much
26 Feb 2010 at 9:05 am [Comment permalink]
Thanks, Samar. Glad you find it useful.
22 Nov 2011 at 5:20 pm [Comment permalink]
it is an excellent site ant it is very useful to me. i found that this site is very useful for all the maths teachers to strengthen their capacity.
1 Jul 2012 at 8:02 pm [Comment permalink]
i am a engineering math Prof... i really found a great benefit reading.. and reading the given information.. I am so happy to join this site..
Thank you so much
9 Oct 2013 at 8:42 pm [Comment permalink]
Excellent explanation.
3 Sep 2014 at 12:17 am [Comment permalink]
Great way of putting it.... Thanks...
2 Feb 2015 at 8:04 am [Comment permalink]
Excellent explanation. Really helpful. Searched so many books and sites but found this extremely helpful...
2 Feb 2015 at 9:17 am [Comment permalink]
@Moon, Bala, Andrew, Sanjay and Muthulakshmi: I'm glad you all found the article useful!
16 Jun 2015 at 4:08 pm [Comment permalink]
Hi,
First up, this is one the best explanations available on the Internet. I mean Math is a beautiful subject which is in sync with things around us and examples such as the one above drive the point home in such simple language. The kids who have the fortune of learning from you will never hate or be fearful of math. Thank you so very much for explaining the concept. I am a Math major and am always looking for alternative/better explanations and I am so glad I found this. I don't just want to be able to solve the problem, I want it to make sense to me intuitively and this did it for me. A lot of professors make it so complex and it almost seems hopelessly abstract. Thanks once again for this explanation.
20 Nov 2015 at 8:35 pm [Comment permalink]
very good explanation
28 Mar 2016 at 5:51 pm [Comment permalink]
The bell-shaped curve doesn't exist!
28 Mar 2016 at 8:18 pm [Comment permalink]
@Tanveer: Thanks for alerting me. The issue has been fixed.
14 Oct 2016 at 10:20 pm [Comment permalink]
Hi, suppose you have been given sides a,b,c and angles A,B,C of a plane triangle vary in such a way that its circum radius remains constant. How do we proove that
da/cosA + db/cosB + dc/cosC = 0
15 Oct 2016 at 9:03 am [Comment permalink]
@Victor: Such questions are best asked on the IntMath Forum. Here's the appropriate section: https://www.intmath.com/forum/differential-equations-32/
28 Jun 2017 at 5:52 am [Comment permalink]
Really helpful explanation. Thank you
28 Oct 2017 at 8:23 pm [Comment permalink]
Thank you very much to the questioner for asking such a simple but important question. And thank you to the answers and comments about this topic.
This is extremely fantastic answer which has cleared lots of misconceptions and doubts about the partial differentiation.
Thanks and stay blessed.
1 Feb 2019 at 6:28 pm [Comment permalink]
thank you !! I never tried to understand the concept before !! But today when i googled it, found this wonderful email.. you wrote to your reader.